Simplificación de una expresión algebraica I

Los exponentes pueden ser adjuntados a variables así como a números. Cuando esto sucede, las reglas básicas de los exponentes y las de la notación exponencial se aplican cuando se escriben y simplifican expresiones algebraicas que contienen exponentes.

Reglas Simples de Exponentes

Veamos algunas de las reglas básicas de los exponentes.

Cualquier número o variable elevado a la potencia de uno es simplemente el mismo número. De la misma forma, cualquier número o variable que no muestre un exponente se le puede considerar un exponente de 1. Abajo hay algunos ejemplos:

51 = 5

18 = 181

x1 = x

xy = x1y1

Otra regla de los exponentes es que cualquier número distinto de cero o variable elevado a la potencia de 0 es igual a 1. 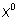  = 1 para x ≠ 0.

Al igual que con los números, las variables elevadas a una potencia negativa equivalen a 1 dividido entre la variable elevada a la misma potencia pero positiva. Por ejemplo:

 

Exponente 0 o 1 y Exponentes Negativos

Cualquier número o variable elevado a la potencia de 1 es el mismo número.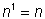  

Cualquier número distinto de cero o variable elevado a la potencia de 0 es igual a 1.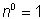    

Cualquier número distinto de cero n y cualquier entero x, 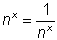. Por ejemplo,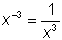

Nota que estas reglas dicen que la base, n, debe ser un "número distinto de cero". Cuando n es 0, n⁰ y n elevados a una potencia negativa no están definidos.

Veamos cómo simplificar una expresión algebraica con exponentes negativos en el numerador y el denominador. Es útil, especialmente al principio, separar las variables y simplificarlas individualmente:

Ejemplo
Problema	Simplificar
		Reescribir como un producto de fracciones
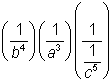		Reescribir las variables con potencias negativas siguiendo la regla de los exponentes negativos:
		Simplificar la división entre una fracción
		Multiplicar las fracciones
Solución