En matemáticas , el teorema de Eisenstein , en honor al matemático alemán Gotthold Eisenstein , se aplica a los coeficientes de cualquier serie de potencias que es una función algebraica con números racionales coeficientes. A través de la teorema, que es fácilmente demostrable que una función tal como la función exponencial debe ser una función trascendental .
Supongamos, por tanto, que
es una serie formal con coeficientes racionales una N , que tiene un no-cero radio de convergencia en el plano complejo , y dentro de ella representa una función analítica que es de hecho una función algebraica. Deje d n denotar el denominador de una n , como una fracción en su mínima expresión . Entonces el teorema de Eisenstein afirma que existe un conjunto finito S de números primos p , de modo que todos los factores primos de un número d n figura en el S .
Esto tiene una interpretación en términos de números p-adic : con una extensión adecuada de la idea, el p -adic radio de convergencia de la serie es de al menos 1, para casi todos los p (es decir, los números primos fuera del conjunto finito S ). De hecho esta declaración es un poco más débil, en que no tiene en cuenta cualquier inicial suma parcial de la serie, en una forma que puede variar de acuerdo con p . Para los otros números primos el radio es distinto de cero.
El artículo original de Eisenstein es la comunicación a corta Über eine der allgemeine Eigenschaft Reihen-Entwicklungen aller algebraischen Functionen (1852), reproducido en Mathematische Gesammelte Werke, Band II, Chelsea Publishing Co., New York, 1975, p. 765-767.
Más recientemente, muchos autores han investigado los límites precisos y eficaces que cuantifiquen las anteriores casi todos . Véase, por ejemplo, las secciones 11.4 y 11.55 del libro de E. Bombieri y W. Gubler.,
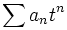
No hay comentarios:
Publicar un comentario