Un planímetro (también conocido como un platometer ) es un instrumento de medida utilizado para determinar el área de una forma bidimensional arbitrario.
Principio del planímetro lineal
El funcionamiento de la planímetro lineal puede ser explicado mediante la medición del área de un rectángulo ABCD (ver la imagen). Se mueve con el puntero de A a B el brazo EM se mueve a través del paralelogramo amarillo, con un área igual a PQ × EM. Esta área también es igual al área del paralelogramo Un "ABB". La rueda de medición mide la distancia PQ (perpendicular a EM). Pasar de C a D el brazo EM se mueve a través del paralelogramo verde, con un área igual al área del rectángulo D "DCC". La rueda de medición se mueve ahora en la dirección opuesta, restando esta lectura de la anterior. El resultado neto es la medición de la diferencia de las áreas de color amarillo y verde, que es el área de ABCD. Hay, por supuesto, los movimientos a lo largo de BC y DA, pero como son el mismo pero de sentido opuesto, que se anulan entre sí en la lectura de la rueda.
Derivación matemática
La operación de un planímetro lineal se puede justificar mediante la aplicación de teorema de Green en los componentes del vector de campo N, dada por:
donde b es la coordenada y del codo E.
Este campo vector es perpendicular a la EM brazo de medición:
y tiene un tamaño constante, igual a la longitud m del brazo de medición:
Entonces:
debido a que:
El lado izquierdo de la ecuación anterior, que es igual a la zona A delimitada por el contorno, es proporcional a la distancia medida por la rueda de medición, con el factor de proporcionalidad m , la longitud del brazo de medición.
Las coordenadas polares
La conexión con el teorema de Green puede ser entendida en términos de integración en coordenadas polares: en coordenadas polares, el área se calcula mediante la integral  donde la forma está integrado es cuadrática en r, lo que significa que la velocidad a la que los cambios de la zona con respecto al cambio en el ángulo de varía cuadráticamente con el radio.
donde la forma está integrado es cuadrática en r, lo que significa que la velocidad a la que los cambios de la zona con respecto al cambio en el ángulo de varía cuadráticamente con el radio.
 donde la forma está integrado es cuadrática en r, lo que significa que la velocidad a la que los cambios de la zona con respecto al cambio en el ángulo de varía cuadráticamente con el radio.
donde la forma está integrado es cuadrática en r, lo que significa que la velocidad a la que los cambios de la zona con respecto al cambio en el ángulo de varía cuadráticamente con el radio.
Para una ecuación paramétrica en coordenadas polares, donde tanto r y θ varían como una función del tiempo, esto se convierte
Para un planímetro polar la rotación total de la rueda es proporcional a  como la rotación es proporcional a la distancia recorrida, que en cualquier punto en el tiempo es proporcional al radio y al cambio en el ángulo, como en la circunferencia de un círculo (
como la rotación es proporcional a la distancia recorrida, que en cualquier punto en el tiempo es proporcional al radio y al cambio en el ángulo, como en la circunferencia de un círculo ( 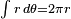 ).
).
 como la rotación es proporcional a la distancia recorrida, que en cualquier punto en el tiempo es proporcional al radio y al cambio en el ángulo, como en la circunferencia de un círculo (
como la rotación es proporcional a la distancia recorrida, que en cualquier punto en el tiempo es proporcional al radio y al cambio en el ángulo, como en la circunferencia de un círculo ( 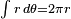 ).
).
Esta última integrando 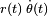 puede ser reconocido como el derivado del integrando anteriormente
puede ser reconocido como el derivado del integrando anteriormente 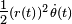 (con respecto a r ), y muestra que un planímetro polar calcula el área integral en términos de la derivada , que se refleja en el teorema de Green, lo que equivale una integral de línea de un función en una (1-dimensional) de contorno a la (2-dimensional) integral de la derivada.
(con respecto a r ), y muestra que un planímetro polar calcula el área integral en términos de la derivada , que se refleja en el teorema de Green, lo que equivale una integral de línea de un función en una (1-dimensional) de contorno a la (2-dimensional) integral de la derivada.
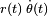 puede ser reconocido como el derivado del integrando anteriormente
puede ser reconocido como el derivado del integrando anteriormente 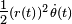 (con respecto a r ), y muestra que un planímetro polar calcula el área integral en términos de la derivada , que se refleja en el teorema de Green, lo que equivale una integral de línea de un función en una (1-dimensional) de contorno a la (2-dimensional) integral de la derivada.
(con respecto a r ), y muestra que un planímetro polar calcula el área integral en términos de la derivada , que se refleja en el teorema de Green, lo que equivale una integral de línea de un función en una (1-dimensional) de contorno a la (2-dimensional) integral de la derivada.



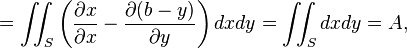
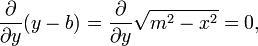


No hay comentarios:
Publicar un comentario