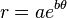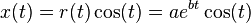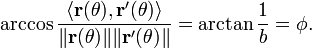sábado, 8 de marzo de 2014
viernes, 7 de marzo de 2014
ELIPSOIDE
Un elipsoide es un tipo de superficie cuádrica que es un análogo dimensional superior de una elipse. La ecuación de un cuerpo elipsoide estándar alineado con el eje en una xyz sistema de coordenadas cartesiano es-
donde una x y un y son el transversal, radios ecuatorial (a lo largo de las x y Y ejes) y b es el conjugado, el radio polar (a lo largo del z -axis), todos los cuales se fijan los números reales positivos que determinan la forma del elipsoide (tradicionalmente, un x y un Y se indican como un y b , respectivamente, - definiendo de este modo el ecuador como una elipse - y B como C , sin embargo, en la mayoría de los casos - como la Tierra - el ecuador se considera esférica, con el radio ecuatorial se define simplemente como un y el polo como b - como una elipse - por lo tanto un , b , c notación puede ser innecesariamente confuso).
Más generalmente, un elipsoide no-necesariamente-alineado con el eje se define por la ecuación
donde A es una matriz definida positiva y simétrica x es un vector. En ese caso, los vectores propios de A definen las direcciones principales de la elipsoide y el inverso de la raíz cuadrada de los valores propios son los correspondientes radios ecuatoriales.
Si todos los tres radios son iguales, el cuerpo sólido es una esfera; si dos radios son iguales, el elipsoide es un esferoide:
 Esfera ;
Esfera ; Esferoide oblato , o oblatum (en forma de disco);
Esferoide oblato , o oblatum (en forma de disco); Prolato esferoide o prolatum (como una pelota de rugby);
Prolato esferoide o prolatum (como una pelota de rugby); Escalenos elipsoide ("tres lados desiguales").
Escalenos elipsoide ("tres lados desiguales").
Los puntos ( una x , 0,0), (0, una Y , 0) y (0,0, b ) se encuentran en la superficie y los segmentos de línea desde el origen a estos puntos se llaman los ejes semi-principales . Estos corresponden a la semi-eje mayor y semi-eje menor de los appropriateellipses.
Elipsoides escalenos son frecuentemente llamados "elipsoides triaxiales", lo que implica que los tres ejes deben especificarse para definir la forma.
PARAMETRIZACIÓN
Utilizando las coordenadas comunes, si  es reducida, o de un punto paramétrico de latitud y
es reducida, o de un punto paramétrico de latitud y  es su longitud planetographic , un elipsoide se puede parametrizar.
es su longitud planetographic , un elipsoide se puede parametrizar.
 es reducida, o de un punto paramétrico de latitud y
es reducida, o de un punto paramétrico de latitud y  es su longitud planetographic , un elipsoide se puede parametrizar.
es su longitud planetographic , un elipsoide se puede parametrizar.VOLUMEN
El volumen de un elipsoide está dada por la fórmula
Tenga en cuenta que esta ecuación se reduce a la del volumen de una esfera cuando todos los tres radios elípticas son iguales, y a la de un esferoide achatado o alargado cuando dos de ellos son iguales.
De área de superficie
El área de la superficie de un elipsoide está dada por:
donde
es el ángulo modular, o excentricidad angular ;  , y
, y  ,
,  son las integrales elípticas incompletas de la primera y segunda clase.
son las integrales elípticas incompletas de la primera y segunda clase.
 , y
, y  ,
,  son las integrales elípticas incompletas de la primera y segunda clase.
son las integrales elípticas incompletas de la primera y segunda clase.
En el caso de un esferoide, la anterior se simplifica a las expresiones de forma cerrada:
- Oblato:
 prolato:
prolato: 
Una fórmula aproximada para cualquier elipsoide es:
Donde p ≈ 1,6075 produce un error relativo de a lo sumo 1,061% (fórmula de Knud Thomsen); un valor de p = 8/5 = 1,6 es óptimo para elipsoides casi esféricas, con un error relativo de a lo sumo 1,178% (David W. Cantrell fórmula).
En el límite de "plano" de  la zona es de aproximadamente
la zona es de aproximadamente  , o más precisamente,
, o más precisamente,
 la zona es de aproximadamente
la zona es de aproximadamente  , o más precisamente,
, o más precisamente,
que, para un esferoide, se reduce a

Propiedades de masa
La masa de un elipsoide de densidad uniforme es:
donde  es la densidad.
es la densidad.
 es la densidad.
es la densidad.
Los momentos de inercia de un elipsoide de densidad uniforme son:
donde  ,
,  y
y  son los momentos de inercia sobre las x , y y z ejes, respectivamente. Productos de inercia son cero.
son los momentos de inercia sobre las x , y y z ejes, respectivamente. Productos de inercia son cero.
 ,
,  y
y  son los momentos de inercia sobre las x , y y z ejes, respectivamente. Productos de inercia son cero.
son los momentos de inercia sobre las x , y y z ejes, respectivamente. Productos de inercia son cero.
Se puede demostrar fácilmente que si un x = a y = b , entonces los momentos de inercia se reducen a las de una esfera uniforme densidad.
A la inversa, si se conocen las inercias de masas y el principio de un cuerpo rígido arbitraria, un elipsoide equivalente de densidad uniforme se puede construir, con las siguientes características:




EQUILIBRIO RATATIONAL
Elipsoides escalenos y cuboides rotan de manera estable a lo largo de sus ejes mayores o menores, pero no a lo largo de su eje medio. Esto se puede ver experimentalmente lanzando una goma de borrar y muchos efectos. Además, momento de inercia consideraciones significa que la rotación a lo largo del eje mayor es más fácilmente perturbado que la rotación a lo largo del eje menor. Un efecto práctico de esto es que los cuerpos astronómicos escalenos como generalmente rotan a lo largo de sus ejes menores (como lo hace la Tierra, que es meramente achatado) y, además, debido a la fijación de marea, lunas escalenos en órbita sincrónica, tales como los de la órbita de Saturno con su eje mayor alineado radialmente a su planeta.
Un elipsoide relajado, es decir, uno en equilibrio hidrostático, tiene un achatamiento un x - B directamente proporcional a su densidad media y la radio medio. Elipsoides con una diferenciada interior, es decir, un núcleo más denso que el manto tiene un achatamiento menor que un cuerpo homogéneo. En general, la relación ( un Y -B ) / ( un x -b ) es de aproximadamente 0,25, aunque esto gotas para los cuerpos que giran rápidamente.
TRANSFORMACIÓN LINEAL
Si se aplica una transformación lineal invertible a una esfera, se obtiene un elipsoide, sino que se puede poner en la forma estándar por encima por una rotación adecuada, una consecuencia del teorema espectral. Si la transformación lineal está representado por una matriz simétrica 3-por-3, entonces los vectores propios de la matriz son ortogonales (debido al teorema espectral) y representan las direcciones de los ejes del elipsoide: las longitudes de los semiejes se dan por los valores propios.
La intersección de un elipsoide con un plano está vacío, un único punto, o una elipse (incluyendo un círculo).
También se puede definir elipsoides en las dimensiones más altas, como las imágenes de las esferas bajo transformaciones lineales invertibles. El teorema espectral de nuevo se puede utilizar para obtener una ecuación estándar similar a la dada anteriormente.
FORMA DE HUEVO
La forma de un huevo de gallina es de aproximadamente la mitad que la de cada una alargada y más o menos esférica (achatado, potencialmente, incluso minorly) elipsoide unido en el ecuador, compartiendo un eje principal de simetría rotacional. Aunque el término en forma de huevo- por lo general implica una falta de simetría de reflexión a través del plano ecuatorial, también puede referirse a los verdaderos elipsoides alargados. También se puede utilizar para describir la figura 2D que, giraba en torno a su eje mayor, produce la superficie 3D. Ver también ovalada.
GOMBOC
Un Gomboc o Gomboc es un cuerpo homogéneo de tres dimensiones convexa que, al descansar sobre una superficie plana, tiene sólo una estable y un punto de equilibrio inestable. Su existencia fue conjeturado por el matemático ruso Vladimir Arnold en 1995 y demostrado en 2006 por científicos húngaros Gábor Domokos y Péter Varkonyi. La forma Gomboc no es único, sino que tiene un sinnúmero de variedades, la mayoría de los cuales están muy cerca de una esfera y todos tienen muy estricta tolerancia de forma (aproximadamente 0,1 mm por 10 cm). La solución más famoso tiene una parte superior afilada y se muestra a la derecha.Su forma ayudó a explicar la estructura de la carrocería de algunas tortugas en relación a su capacidad para volver a la posición de equilibrio después de haber sido colocado al revés. Copias de Gomboc han sido donados a instituciones y museos, y el mayor de ellos fue presentado en la Expo Mundial 2010 en Shanghai, China.
Historia
En geometría, un cuerpo con una sola posición de reposo estable se llama monoestático , y el término mono-monoestático se ha acuñado para describir un cuerpo que, además, tiene un solo punto de equilibrio inestable. (El poliedro monoestático anteriormente conocido no calificar, ya que tiene tres equilibrios inestables.) Una esfera ponderados para que itscenter de masa se desplaza desde el centro geométrico es un cuerpo-mono monoestático. Un ejemplo más común es el Comeback Kid, juguete Weeble o brazo de gitano (ver figura de la izquierda). No sólo tienen un bajo centro de gravedad, sino que también tiene una forma específica. En el equilibrio, el centro de masa y el punto de contacto están en la línea perpendicular al suelo. Cuando se empuja el juguete, su centro de subidas masivas y también se aleja de esa línea. Esto produce un momento de enderezamiento que devuelve el juguete a la posición de equilibrio.
Los ejemplos anteriores de los objetos mono-monoestático son necesariamente no homogénea, es decir, la densidad de su material varía a través de su cuerpo. La cuestión de si es posible construir un cuerpo tridimensional que es mono-monoestático sino también homogénea y convexa fue planteada por el matemático ruso Vladimir Arnoldin 1995. El requisito de ser convexa es esencial, ya que es trivial para la construcción de un cuerpo no convexo-mono monoestático.Convexo significa que cualquier línea recta entre dos puntos de un cuerpo se encuentra en el interior del cuerpo, o, en otras palabras, que la superficie no tiene regiones hundidas pero en lugar sale hacia el exterior (o es al menos plana) en cada punto. Ya era bien conocido, a partir de una generalización geométrica y topológica de la clásica teorema de los cuatro vértices, que una curva plana tiene al menos cuatro extremos de curvatura, específicamente, al menos dos máximos locales y al menos dos mínimos locales (ver figura de la derecha) , lo que significa que un (convexa) objeto mono-monoestático no existe en dos dimensiones. Mientras que una expectativa común era que un cuerpo tridimensional también debe tener por lo menos cuatro extremos, Arnold conjetura que este número podría ser menor.
Solución matemática
El problema fue resuelto en 2006 por Gábor Domokos y Péter Várkonyi. Domokos es ingeniero y es el jefe de Mecánica, Materiales y Estructuras en la Universidad de Budapest de Tecnología y Economía. Desde 2004, es el miembro más joven de la Academia Húngara de Ciencias. Várkonyi se formó como arquitecto, era un estudiante de Domokos y medallista de plata en la Olimpiada Internacional de Física en 1997. Después de permanecer como estudiante de post-doctorado en la Universidad de Princeton, en 2006-2007, asumió una posición de profesor asistente en la Universidad de Budapest de Tecnología y Economía. Domokos previamente había estado trabajando en los organismos mono-monoestático. En 1995 conoció a Arnold en una importante conferencia de matemáticas en Hamburgo, donde Arnold presentó una charla plenaria que demuestra que la mayoría de los problemas geométricos tienen cuatro soluciones o puntos extremales. En una conversación personal, sin embargo, Arnold cuestionó que cuatro es un requisito para los organismos mono-monoestático y alentó Domokos a buscar ejemplos con un menor número de equilibrios.
La prueba rigurosa de la solución se puede encontrar en las referencias de su trabajo. El resumen de los resultados es que el cuerpo tridimensional homogénea convexa (mono-monoestático), que tiene una estable y un punto de equilibrio inestable, existe y no es único. Estos organismos son difíciles de visualizar, describir o identificar. Su forma es muy diferente a cualquier representante típico de cualquier otra clase geométrica equilibrio. Deben tener "planitud" mínima y, para evitar tener dos equilibrios inestables, también debe tener "delgadez" mínima. Ellos son los únicos objetos no degenerados que tienen planitud simultáneamente mínimo y la delgadez. La forma de los cuerpos es muy sensible a pequeñas variaciones, fuera de la cual ya no es mono-monoestático. Por ejemplo, la primera solución de Domokos y Várkonyi se parecía mucho a una esfera, con una desviación forma de sólo 10 -5 . Fue despedido, ya que era muy difícil de probar experimentalmente. Su solución fue publicado menos sensible; sin embargo, tiene una tolerancia de forma de 10 -4 , es decir 0,1 mm para un tamaño de 10 cm.
Domokos y su esposa desarrollaron un sistema de clasificación de las formas en función de sus puntos de equilibrio mediante el análisis de guijarros y tomando nota de sus puntos de equilibrio. En un experimento, se trataron 2.000 guijarros recogidos en las playas de la isla griega de Rodas y no encontraron un solo cuerpo-mono monoestático entre ellos, lo que demuestra la dificultad de encontrar o construir ese órgano.
La solución de Domokos y Várkonyi tiene bordes curvos y se asemeja a una esfera con una tapa aplastada. En la figura superior, se basa en su equilibrio estable. Su posición de equilibrio inestable se obtiene mediante la rotación de la figura 180 ° alrededor de un eje horizontal. Teóricamente, éste descanse allí, pero la perturbación más pequeña lo traerá de vuelta al punto estable. El Gomboc matemático tiene en efecto esfera-como propiedades. En particular, su planitud y la delgadez son mínimos, y este es el único tipo de objeto no degenerado con esta propiedad. Domokos y Várkonyi están interesados en encontrar una solución poliédrica con la superficie que consta de un número mínimo de planos lisos. Por lo tanto, ofrecen un premio a cualquier persona que encuentre a esa solución, lo que equivale a $ 10.000, dividido por el número de aviones en la solución. Obviamente, se puede aproximar sus Gomboc curvilínea con un número finito de superficies discretas, sin embargo, su estimación es que tomará miles de aviones para lograrlo. Tienen la esperanza, al ofrecer este premio, para estimular la búsqueda de una solución radicalmente distinta a la suya.
Nombre
Si se analiza cuantitativamente en términos de planeidad y de espesor, el cuerpo mono-monoestático descubierto es la más cuerpo de esfera, aparte de la esfera misma. Debido a esto, fue nombrado Gomboc, es decir, un diminutivo de gömb ("esfera" en húngaro). Originalmente Gomboc es una forma de salchicha de alimentos: carne de cerdo sazonada rellenado cerdo estómago, similar a haggis. Hay un cuento popular húngaro sobre un Gomboc antropomórfico, que se traga a varias personas en conjunto.
ESPIRAL
Una espiral logarítmica , espiral equiangular o espiral de crecimiento es una curva espiral auto-similar que a menudo aparece en la naturaleza. La espiral logarítmica fue descrita por primera byDescartes y posteriormente investigado extensivamente por Jacob Bernoulli, quien lo llamó mirabilis Spira , "la espiral maravillosa".
Definición
En coordenadas polares  de la curva logarítmica se puede escribir como
de la curva logarítmica se puede escribir como
 de la curva logarítmica se puede escribir como
de la curva logarítmica se puede escribir como
o
con  ser la base de los logaritmos naturales,
ser la base de los logaritmos naturales,  y
y  ser constantes reales positivas arbitrarias.
ser constantes reales positivas arbitrarias.
 ser la base de los logaritmos naturales,
ser la base de los logaritmos naturales,  y
y  ser constantes reales positivas arbitrarias.
ser constantes reales positivas arbitrarias.
En forma paramétrica, la curva es
con números reales  y
y  .
.
 y
y  .
.
La espiral tiene la propiedad de que el ángulo φ entre la tangente y la línea radial en el punto  es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
 es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
El derivado de 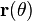 es proporcional al parámetro
es proporcional al parámetro  . En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que
. En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que 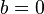 (
( 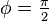 ) la espiral se convierte en un círculo de radio
) la espiral se convierte en un círculo de radio  . Por el contrario, en el límite que
. Por el contrario, en el límite que  se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
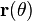 es proporcional al parámetro
es proporcional al parámetro  . En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que
. En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que 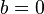 (
( 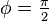 ) la espiral se convierte en un círculo de radio
) la espiral se convierte en un círculo de radio  . Por el contrario, en el límite que
. Por el contrario, en el límite que  se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .Spira mirabilis y Jacob Bernoulli
Spira mirabilis , en latín significa "espiral milagrosa", es otro nombre para la espiral logarítmica. Aunque esta curva ya había sido nombrado por otros matemáticos, el nombre específico (o en espiral "milagrosa" "maravillosa") se le dio a esta curva por Jacob Bernoulli, porque él estaba fascinado por una de sus propiedades matemáticas únicas: el tamaño de la espiral aumenta pero su forma no se altera con cada curva sucesiva, una propiedad conocida como la auto-similitud.Posiblemente como resultado de esta propiedad única, el mirabilis Spira ha evolucionado en la naturaleza, que aparece en ciertas formas de cultivo, tales como conchas de nautilus y jefes de girasol. Jacob Bernoulli quería esa espiral grabada en su lápida junto con la frase "Eadem mutata resurgo" ("Aunque cambiado, he de levantarme de la misma."), Pero, por error, espiral anArchimedean se colocó en su lugar.
Espirales logarítmica en la Naturaleza
En varios fenómenos naturales se pueden encontrar curvas que están cerca de ser espirales logarítmicas. A continuación hay ejemplos y razones:
- El enfoque de un halcón a su presa. Su punto de vista más agudo está en un ángulo a su dirección de vuelo; este ángulo es el mismo que el tono de la espiral.
- El enfoque de un insecto a una fuente de luz. Ellos están acostumbrados a que la fuente de luz en un ángulo constante de su trayectoria de vuelo. Por lo general, el sol (o la luna para especies nocturnas) es la única fuente de luz y volar de esa manera se traducirá en una línea prácticamente recta.
- Los brazos de las galaxias espirales. Nuestra propia galaxia, la Vía Láctea, tiene varios brazos espirales, cada uno de los cuales es aproximadamente una espiral logarítmica con paso de aproximadamente 12 grados.
- Los nervios de la córnea (esto es, los nervios de la córnea de la capa subepitelial terminan cerca de capa epitelial superficial de la córnea en un patrón espiral logarítmica).
- Las bandas de los ciclones tropicales, como los huracanes.
- Muchas estructuras biológicas incluyendo las conchas de los moluscos. En estos casos, la razón puede ser la construcción de la expansión de formas similares, como se muestra cifras forpolygonal en el gráfico adjunto.
- Playas espiral logarítmica pueden formar como resultado de la refracción y la difracción de la onda por la costa. Half Moon Bay, California es un ejemplo de un tipo de playa tales.
Suscribirse a:
Entradas (Atom)