Una espiral logarítmica , espiral equiangular o espiral de crecimiento es una curva espiral auto-similar que a menudo aparece en la naturaleza. La espiral logarítmica fue descrita por primera byDescartes y posteriormente investigado extensivamente por Jacob Bernoulli, quien lo llamó mirabilis Spira , "la espiral maravillosa".
Definición
En coordenadas polares  de la curva logarítmica se puede escribir como
de la curva logarítmica se puede escribir como
 de la curva logarítmica se puede escribir como
de la curva logarítmica se puede escribir como
o
con  ser la base de los logaritmos naturales,
ser la base de los logaritmos naturales,  y
y  ser constantes reales positivas arbitrarias.
ser constantes reales positivas arbitrarias.
 ser la base de los logaritmos naturales,
ser la base de los logaritmos naturales,  y
y  ser constantes reales positivas arbitrarias.
ser constantes reales positivas arbitrarias.
En forma paramétrica, la curva es
con números reales  y
y  .
.
 y
y  .
.
La espiral tiene la propiedad de que el ángulo φ entre la tangente y la línea radial en el punto  es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
 es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
es constante. Esta propiedad se puede expresar en términos geométricos diferenciales como
El derivado de 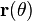 es proporcional al parámetro
es proporcional al parámetro  . En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que
. En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que 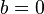 (
( 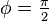 ) la espiral se convierte en un círculo de radio
) la espiral se convierte en un círculo de radio  . Por el contrario, en el límite que
. Por el contrario, en el límite que  se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
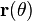 es proporcional al parámetro
es proporcional al parámetro  . En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que
. En otras palabras, se controla la "fuerza" y en qué dirección las espirales en espiral. En el caso extremo de que 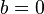 (
( 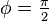 ) la espiral se convierte en un círculo de radio
) la espiral se convierte en un círculo de radio  . Por el contrario, en el límite que
. Por el contrario, en el límite que  se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .
se acerca al infinito ( Phi → 0) la espiral tiende hacia un medio en línea recta.Thecomplement de φ se llama el terreno de juego .Spira mirabilis y Jacob Bernoulli
Spira mirabilis , en latín significa "espiral milagrosa", es otro nombre para la espiral logarítmica. Aunque esta curva ya había sido nombrado por otros matemáticos, el nombre específico (o en espiral "milagrosa" "maravillosa") se le dio a esta curva por Jacob Bernoulli, porque él estaba fascinado por una de sus propiedades matemáticas únicas: el tamaño de la espiral aumenta pero su forma no se altera con cada curva sucesiva, una propiedad conocida como la auto-similitud.Posiblemente como resultado de esta propiedad única, el mirabilis Spira ha evolucionado en la naturaleza, que aparece en ciertas formas de cultivo, tales como conchas de nautilus y jefes de girasol. Jacob Bernoulli quería esa espiral grabada en su lápida junto con la frase "Eadem mutata resurgo" ("Aunque cambiado, he de levantarme de la misma."), Pero, por error, espiral anArchimedean se colocó en su lugar.
Espirales logarítmica en la Naturaleza
En varios fenómenos naturales se pueden encontrar curvas que están cerca de ser espirales logarítmicas. A continuación hay ejemplos y razones:
- El enfoque de un halcón a su presa. Su punto de vista más agudo está en un ángulo a su dirección de vuelo; este ángulo es el mismo que el tono de la espiral.
- El enfoque de un insecto a una fuente de luz. Ellos están acostumbrados a que la fuente de luz en un ángulo constante de su trayectoria de vuelo. Por lo general, el sol (o la luna para especies nocturnas) es la única fuente de luz y volar de esa manera se traducirá en una línea prácticamente recta.
- Los brazos de las galaxias espirales. Nuestra propia galaxia, la Vía Láctea, tiene varios brazos espirales, cada uno de los cuales es aproximadamente una espiral logarítmica con paso de aproximadamente 12 grados.
- Los nervios de la córnea (esto es, los nervios de la córnea de la capa subepitelial terminan cerca de capa epitelial superficial de la córnea en un patrón espiral logarítmica).
- Las bandas de los ciclones tropicales, como los huracanes.
- Muchas estructuras biológicas incluyendo las conchas de los moluscos. En estos casos, la razón puede ser la construcción de la expansión de formas similares, como se muestra cifras forpolygonal en el gráfico adjunto.
- Playas espiral logarítmica pueden formar como resultado de la refracción y la difracción de la onda por la costa. Half Moon Bay, California es un ejemplo de un tipo de playa tales.
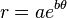

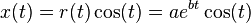

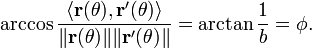




No hay comentarios:
Publicar un comentario