Fue planteada por David Hilbert en la conferencia de París del Congreso Internacional de Matemáticos en el año 1900, como parte de su lista de 23 problemas de matemáticas.
El problema original se hizo pasar por el problema de la topología de curvas y superficies algebraicas ( Problema der Topologie algebraischer Kurven und Flächen ).
En realidad, el problema consiste en dos problemas similares en diferentes ramas de las matemáticas:
- Una investigación de las posiciones relativas de las ramas de las curvas algebraicas reales de grado n (y de manera similar para superficies algebraicas).
- La determinación del límite superior para el número de ciclos límite en campos de vectores polinomiales de dos dimensionial de grado n y el análisis de sus posiciones relativas.
El primer problema es aún sin resolver para n = 8. Por lo tanto, este problema es lo que generalmente se entiende cuando se habla de un problema decimosexta de Hilbert en la geometría algebraica real. El segundo problema también sigue sin resolverse: no límite superior para el número de ciclos límite se conoce para cualquier n > 1, y esto es lo que normalmente se entiende por problema decimosexta de Hilbert en el campo de los sistemas dinámicos.
LA PRIMERA PARTE DEL PROBLEMA DE HILBERT.
En 1876 Harnack investigó las curvas algebraicas en el plano proyectivo real y encontró que las curvas de grado n no podían tener más de
componentes conectados separados. Además, mostró cómo construir curvas que alcanzado ese límite superior, y por lo tanto que era la mejor posible salto. Curvas con ese número de componentes son calledM curvas.
Hilbert había investigado los M-curvas de grado 6, y encontraron que los componentes 11 siempre se agrupan de una manera determinada.Su reto a la comunidad matemática ahora fue investigar completamente las posibles configuraciones de los componentes de la M-curvas.
Además solicitó una generalización del teorema de Harnack a superficies algebraicas y una investigación similar de las superficies con el máximo número de componentes.
LA SEGUNDA PARTE DEL PROBLEMA DE HILBERT
Aquí vamos a considerar los campos de vectores polinomiales en el plano real, es decir un sistema de ecuaciones diferenciales de la forma:
donde ambos P y Q son polinomios reales de grado n .
Estos campos de vectores polinomiales fueron estudiados por Poincaré, quien tuvo la idea de abandonar la búsqueda de encontrar soluciones exactas para el sistema, y en su lugar trató de estudiar las características cualitativas de la colección de todas las soluciones posibles.
Entre los muchos descubrimientos importantes, se encontró que los conjuntos límite de este tipo de soluciones no deben ser un punto estacionario, sino que más bien podría ser una solución periódica. Este tipo de soluciones se llaman ciclos límite.
La segunda parte del problema 16a de Hilbert es decidir un límite superior para el número de ciclos límite en los campos de vectores polinomio de grado n y, de forma similar a la primera parte, investigar sus posiciones relativas.
RESULTADOS.
Se mostró en 1991/1992 por Yulii Ilyashenko y Jean Ecalle que cada campo vectorial polinomio en el avión sólo tiene un número finito de ciclos límite (un artículo de 1923 por Henri Dulac reclamando una prueba de esta afirmación se ha demostrado que contienen un vacío en 1981) . Esta declaración no es evidente, ya que es fácil de construir (C lisas ∞ campos) de vectores en el plano con un número infinito de ciclos límite concéntricos.
La cuestión de si existe un límite superior finito H ( n ) para el número de ciclos límite de los campos de vectores polinomiales planas de grado n sigue sin resolverse para cualquier n > 1. ( H (1) = 0, ya que los campos vectoriales lineales no tienen ciclos límite.) Evgenii Landis e Iván Petrovsky reclamado una solución en la década de 1950, pero se demostró equivocada en la década de 1960. Campos avión vector cuadráticas con cuatro ciclos límite son conocidos.
LA FORMULACIÓN ORIGINAL DE LOS PROBLEMAS.
En su discurso, Hilbert presentó los problemas como:
| Las ramas atadas de cerrado y separado superiores de una curva algebraica de grado n se decidió por Harnack (Mathematische Annalen, 10), a partir de esto surge la pregunta aún más a partir de las posiciones relativas de las sucursales en las plane.As de las curvas de nivel 6, no tengo - ciertamente de una manera bastante elaborada - convencí a mí mismo de que las 11 ramas, que pueden tener de acuerdo con Harnack, no todos pueden estar separados, en lugar debe existir una rama, que tienen otra sucursal corriendo en su interior y nueve ramas que se ejecutan en su exterior, o lo contrario. Me parece que una investigación a fondo de las posiciones relativas de la cota superior de ramas separadas es de gran interés, y del mismo modo la investigación correspondiente del número, la forma y la posición de las hojas de una superficie algebraica en el espacio - que aún no es incluso conocido, la cantidad de hojas una superficie de grado 4 en el espacio tridimensional puede tener al máximo. (Cf. Rohn, Flächen vierter Ordnung, Preissschriften der Fürstlich Jablonowskischen Gesellschaft, Leipzig 1886) |
Hilbert sigue:
| A raíz de este problema puramente algebraica me gustaría plantear una pregunta que, me parece, puede ser atacado por el mismo método de cambio de coeficiente de continua, y cuya respuesta es de una importancia similar a la topología de las familias de curvas definidas por ecuaciones diferenciales - esa es la cuestión de la posición de encuadernado y la parte superior de los ciclos límite Poincaré (ciclos) Limites de una ecuación diferencial de primer orden de la forma:
donde X , Y son enteros, funciones racionales de n . º grado en resp x , Y , o escrito de forma homogénea: donde X , Y , Z significa integrales racionales, funciones, Homogenic de n º grado en x , y , z y la última se han de considerar en función del parámetro t .
|


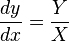
No hay comentarios:
Publicar un comentario