Aunque no existe un concenso general sobre cuál de los problemas abiertos en matemáticas es el más importante, muchos creen que el más famoso es la Hipótesis de Riemann. Esto se sustenta en 3 cosas: 

1. Es uno de las conjeturas más fáciles de comprender, pero una de las más difíciles de demostrar. Así mismo es uno de los problemas no-resueltos de las matemáticas más antiguos.

2. Dado que se trata de uno de los Problemas del Milenio y que está entre las cuestiones matemáticas más profundas, complejas y desafiantes para los expertos, se ha ofrecido un premio de un millón de dólares por el Instituto Clay de Matemáticas para la primera persona que desarrolle una demostración correcta de la conjetura. 

3.Dicha conjetura fue formulada en 1859, en una época donde se tenía la impresión de no poder ver los límites del análisis matemático, por lo que Hilbert (célebre matemático alemán) y muchos otros creyeron que la hipótesis se resolvería en 10 años. Sin embargo la demostración resultó demasiado difícil para los matemáticos, por lo que Hilbert dijo poco antes de morir que, si lo resucitaran 500 años después, lo primero que preguntaría sería: “¡¿Alguien resolvió la hipótesis de Riemann?!”. Al día de hoy, nadie ha podido resolverla. 

La Hipótesis de Riemann

La conjetura de Riemann afirma que:

La parte real de todo cero no trivial de la función zeta de Riemann es 1/2

Para empezar, la función zeta se define como:

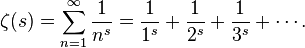
La letra griega sigma Σ es un operador matemático que permite representar sumas de muchos sumandos incluso infinitos sumandos. Por ejemplo, si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:

Sin embargo, esta función no es válida para todos los valores, ya que algunos "divergen", es decir, calculan resultados infinitos. Ejemplo:

Sin embargo, los matemáticos han desarrollado una técnica para 2sumar"; números infinitos. A pesar de que la suma 1+2+3+4+... puede parecer que a primera vista no tiene ningún valor significativo, puede ser manipulado para producir una serie de resultados matemáticos interesantes, algunos de los cuales tienen aplicaciones en otros campos como el análisis complejo, la teoría cuántica de campos y la teoría de cuerdas. 

Esta es una de las cosas más raras de las matemáticas: Para sumar 1+2+3+4+...∞ , los matemáticos elaborararon una técnica que calcula la suma de éstos números al infinito, asignándole a la suma un resultado finito. Esta técnica se aplica comúnmente a problemas de Física, pero tiene su origen en los intentos de dar un significado preciso a la terribles sumas que aparecen en la teoría de números. Aunque tal vez suene muy abstracto e inclusive paradójico, existen algunos ejemplos de ello:

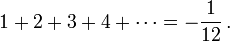
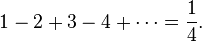
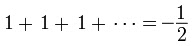
A esto se le conoce como la Regularización de la Función Zeta de Riemann, Como dato adicional, el matemático hindú Ramanujan (1887-1920) llegó a los mismos resultados casi al mismo tiempo de formularse las regularizaciones de la Función Zeta en Occidente, siendo autodidacta y sin tener acceso a trabajos científicos.

Ahora bien, para entender el enunciado, recordemos que todo número se compone de la suma de una parte real y una parte imaginaria, es decir, n = a + b*i, siendo a y b cualquier número real (0, 1, -1, 1/4, π, e, etc.) y i=√-1. Los ceros triviales son aquellos que resultan de calcular la Función Zeta con cualquier número par negativo. Osea que ζ(-2)=0, ζ(-10)=0, ζ(-100)=0

Entonces lo que predice el desquiciado de Riemann es que en la Función Zeta los ceros no triviales deberían encontrarse en la línea crítica 1/2, es decir, que al graficar la Función Zeta, ζ(x) = 1/2 + x*i, las 2 líneas (la real 1/2 y la imaginaria ix) se intersectan en 0. Si graficaramos la Función con 1/3,1/5, etc. las líneas no se intersectarían nunca en 0.

Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011.

La Hipótesis de Riemann fue mencionada en un trabajo de 1859 del matemático alemán Bernhard Riemann,Sobre los números primos menores que una magnitud dada. Surgió colateralmente mientras investigaba algunas de las propiedades de los números primos y tiene como cuestión de fondo su curiosa distribución, si es en cierto modo predecible o no, algo que relacionó con con la llamada función Zeta de Riemann. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración de la misma. La mayoría de la comunidad matemática piensa que la conjetura es cierta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se mostraron escépticos. Los matemáticos confían en que tarde o temprano tendrán éxito en demostrar la hipótesis de Riemann, pero no saben cuanto tiempo les llevará hacerlo.