La hipótesis de Riemann y los números primos

La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos ya que, según el Productorio de Euler, la Función Zeta se puede definir como:

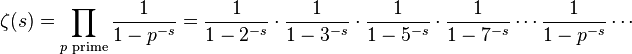
El productorio hace exactamente lo mismo que el sumatorio, sólo que en vez de calcular las sumas, calcula los productos.

Por tanto la hipótesis tiene una estrecha relación con la Conjetura de Goldbach:

Todo número par mayor que 2 puede escribirse como suma de dos números primos.

La cuestión es que no se puede saber si todos los números cumplen con esta conjetura porque los números son infinitos; por tanto habría de formular una ley que los abarcase todos. Sin embargo, no es tan fácil como parece, porque por lo que sabemos, los números primos son muy caprichosos, ya que mientras a lo largo de la recta númerica aparecen en intervalos constantes, en algunos tramos apenas aparecen. La gran mayoría de los matemáticos piensa que al resolverse la Conjetura de Goldbach, se podría resolver la hipótesis de Riemann y viceversa, pero la 2 conjeturas aún están esperando su demostración.

Los intentos de demostrar la hipótesis de Riemann

Varios matemáticos se han ocupado de la hipótesis de Riemann, pero ninguno de sus intentos han sido aceptados como soluciones correctas. 

Investigadores del Consejo Superior de Investigaciones Científicas (CSIC) y la Universidad de Cambridge han dado un nuevo paso hacia la demostración de la Hipótesis. Desde hace algunas décadas los científicos sospechan que es posible demostrar la hipótesis de Riemann desde la física, convirtiendo la función zeta de Riemann -que origina la hipótesis- en una ecuación similar a las usadas en física cuántica, en la que los ceros de la función correspondan a los niveles de energía de un sistema cuántico. Este sistema cuántico que proponen es muy usado en el estudio de determinados fenómenos de materia condensada, por lo que “en principio sería posible construir en laboratorio un sistema cuyo espectro fueran los ceros de Riemann”. Sin embargo, esto no llevaría a una demostración de la hipótesis, que debe hacerse en términos exclusivamente matemáticos. No obstante, contribuirá en el futuro a la solución final y mientras tanto, es algo que ha despertado un gran interés.

En 2008 Xian-Jin Li subó un artículo al arXiv que se titula A proof of Riemann hipothesis (Una demostración de la hipótesis de Riemann) que pretendía ofrecer una solución definitiva a la cuestión. Arxiv.org es una web para publicar trabajos de investigación. Los trabajos que se publican no se someten a ningún tipo de validación, con lo que en este sitio proliferan trabajos sin validez científica y por eso cada semana aparecen en arXiv una prueba sobre la Hipótesis de Riemann, que nunca resulta válida. Una sencilla búsqueda muestra un buen número de estas «pruebas», que duermen allí ignoradas por la comunidad matemática. Y aunque el trabajo de Li prometía ser la excepción, a poco tiempo de ser publicado, llegan las primeras críticas a la prueba de la hipótesis de Riemann. Terence Tao, ganador de la Medalla Fields en 2006, ha escrito un comentario negativo sobre la prueba publicada por el Dr. Li. Alain Connes, también ganador de la Medalla Fields en 1982, ha señalado otros problemas. No habían pasado 72 horas desde la publicación del Dr. Li cuando retira su publicación definitivamente porque no es capaz de responder adecuadamente a la objeción del 2º de sus geniales colegas, siendo él mismo un tipo de primera fila, de la vanguardia de la ciencia.

En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, ya que numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.

Hasta el 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005, y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.

La verificación numérica que muchos ceros se encuentran en la línea a primera vista parece ser una fuerte evidencia de ello. Sin embargo la teoría analítica de números ha tenido muchas conjeturas con el apoyo de grandes cantidades de datos numéricos que resultan ser falsas.

¿Qué pasaría si demostraran la Hipótesis?

Si la hipótesis fuera cierta, las consecuencias serían numerosas en tanto en la Teoría de Números, Física, Estadística, etc:

Siendo que la conjetura está catalogada como uno de los problemas del milenio, el Instituto Clay de Matemáticas estaría obligado a pagarle $1´000,000 de dólares al desquiciado que lograse una correcta demostración de la misma, así como la medalla Fields (equivalente al Nobel en Matemáticas) y fama mundial.

Si la hipótesis de Riemann se cumple, se podrían hacer válidas todas las ecuaciones relacionadas con los números primos. Por ejemplo, la siguiente ecuación es cierta si y sólo si la Hipótesis de Riemann es correcta:

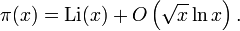
Para finalizar, les presento una aplicación práctica de lo que sería el Teorema de Riemann:

1,000,000,000,000,000 se puede expresar como 10^15

10^80 es el número de protones que hay en el universo conocido.

10^220 a 10^1080 es el tamaño de los números que se usan para codificar la seguridad en las transacciones de internet. Son números gigantescos. Y para codificarlos no sólo se usan números grandes, sino también los números formados al multiplicar los números primos grandes, porque los números primos son el cimiento de las matemáticas. Debido a que se dan en intervalos a lo largo de la línea numérica, es increíblemente difícil separar un número gigante y descomponerlo en sus componentes primos. La seguridad en internet funciona mediante un número primo grande y desconocido oculto dentro de otro número que no se puede descomponer. Por eso se dice que la complejidad es lo que impide descifrar una clave. Ahora bien, si alguien pudiera demostrar la Hipótesis, en base a ello se podría elaborar un algoritmo que permita encontrar los números primos que originaron cualquier clave en internet y entrar en cuentas de Facebook, bancarias y prácticamente cualquier sitio web seguro. Obviamente si antes se publicase la demostración, se desarrollarían nuevos modelos de seguridad para los sitios informáticos.