TEOREMA
DE PITÁGORAS
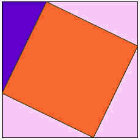
El teorema
de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa ("el lado de mayor longitud del
triángulo rectángulo") es igual a la suma de los cuadrados de los catetos (los
dos lados menores del triángulo, los que conforman el ángulo recto).
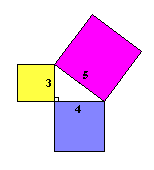
Teorema de Pitágoras
En
todo triángulo rectángulo el cuadrado de
la hipotenusa es igual a la suma de los cuadrados de los catetos.
Pitágoras de Samos
|
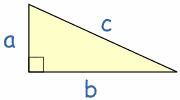
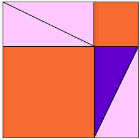
Si un triángulo rectángulo tiene catetos de
longitudes , y la medida de la hipotenusa es
, se establece que:
(1)
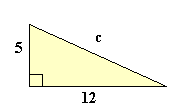
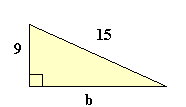
De la ecuación (1) se deducen fácilmente 3 corolarios de aplicación práctica:
El teorema
de Pitágoras tiene este
nombre porque su descubrimiento recae sobre la escuela pitagórica.
Anteriormente, en Mesopotamia y el Antiguo
Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo
rectángulo, y se utilizaban para resolver problemas referentes a los citados
triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga
teóricamente su relación. La pirámide de Kefrén,
datada en el siglo
XXVI a. C., fue la primera gran
pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
El
teorema de Pitágoras es de mucha utilidad en la resolución de problemas de la
vida cotidiana.
Por
ejemplo:
·
El
famoso Galileo Galilei, utilizó
el teorema de Pitágoras para determinar la medida de algunas montañas
lunares.
·
Conocer
la altura de un edificio, sabiendo la medida de la sombra que proyecta y la
distancia del punto más alto del edificio al extremo de la sombra.
·
Se
desean bajar frutos de un árbol de naranjas, para ello se quiere construir una
escalera que sea capaz de alcanzarlos, sabiendo la altura a la que se
encuentran los frutos y la distancia del árbol a la base de la escalera.