NÚMERO DE GRAHAM

Número de Graham , el nombre de Ronald Graham, es un gran número que es un límite superior en la solución a un determinado problema en la teoría de Ramsey.

El número ha subido de grado de atención popular cuando Martin Gardner describió en la sección de "Juegos Matemáticos"  Scientific American  en noviembre de 1977, escrito que, "En una prueba inédita, Graham ha establecido recientemente ... un salto tan grande que tiene el récord para el mayor número jamás utilizada en una prueba matemática seria. "El 1980  del Libro Guinness de los Récords repitió la afirmación de Gardner, quien agregó que el interés popular en este número. Según el físico John Baez, Graham inventó la cantidad que ahora se conoce como el número de Graham en una conversación con el propio Gardner. Mientras que Graham estaba tratando de explicar un resultado en la teoría de Ramsey que había obtenido con su colaborador BL Rothschild, Graham encontró que la cantidad ahora se conoce como número de Graham fue más fácil de explicar que el número real que aparece en el comprobante. Debido a que el número que Graham describe a Gardner es mayor que el número en el propio papel, ambos son límites superiores válidas para la solución al problema de Ramsey-teoría estudiado por Graham y Rothschild.

Número de Graham es inimaginablemente grande que otros grandes números bien conocidos, tales como un googol, googolplex, e incluso más grande que el número de Skewes y número de Moser. De hecho, al igual que los últimos tres de esos números, el universo observable es demasiado pequeño para contener una representación digital común de número de Graham, en el supuesto de que cada dígito ocupa al menos un volumen de Planck. 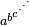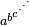Evenpower torres de la forma   no son útiles para este propósito, a pesar de que se puede describir fácilmente mediante fórmulas recursivas utilizando flecha hacia arriba notación de Knuth o su equivalente, como se hizo por Graham. Los diez últimos dígitos del número de Graham son ... 2464195387.

Enteros específicos conocidos por ser mucho más grande que el número de Graham ya han aparecido en muchas demostraciones matemáticas graves (por ejemplo, en relación con diversas formas finitas de Friedman del teorema de Kruskal).