En la geometría hiperbólica, el ángulo de paralelismo φ , también conocido como Π (p), es el ángulo en un vértice de un triángulo hiperbólico derecho que tiene dos lados paralelos asintóticas. El ángulo depende de la longitud de segmento de una entre el ángulo derecho y el vértice del ángulo de paralelismo φ . Dado un punto fuera de la línea, si dejamos caer una perpendicular a la línea desde el punto de, a continuación, una es la distancia a lo largo de este segmento perpendicular, y φ es el menor ángulo de tal manera que la línea que pasa por el punto en el que el ángulo no se cruza la línea dada. Desde dos lados son paralelos asintótica,
Estos cinco expresiones equivalentes relacionan φ y un :
donde gd es la función Gudermannian.
DEMOSTRACIÓN.
En el modelo semi-plano del plano hiperbólico (ver movimientos hiperbólicos) se puede establecer la relación de φ a una geometría euclidiana. Deje que Q sea el semicírculo con un diámetro en el x -eje que pasa por los puntos (1,0) y (0, Y ), donde Y > 1. Puesto que Q es tangente a la unidad de semicírculo centrado en el origen, los dos semicírculos representan líneas hiperbólicas paralelas. El Y -eje cruza ambos semicírculos, haciendo un ángulo recto con la unidad de semicírculo y un ángulo variable φ con Q . El ángulo en el centro de Q subtendido por el área para (0, y ) es también φ debido a que los dos ángulos tienen lados perpendiculares, lado izquierdo al lado izquierdo y el lado derecho al lado derecho. El semicírculo Q tiene su centro en ( x , 0), x <0, por lo que su radio es 1 - x . Por lo tanto, el radio al cuadrado de Q es
por lo tanto
La métrica del modelo de medio-plano de la geometría hiperbólica parametriza distancia en el rayo {(0, Y ): Y > 0} con logaritmo natural.Vamos a iniciar y = a , para y = e un . Entonces la relación entre φ y un se puede deducir de la triángulo {( x , 0), (0, 0), (0, y )}, por ejemplo:

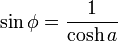
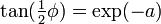


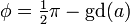
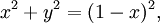

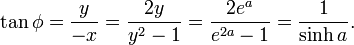
Muy bien, ya te estás acercando al Cálculo!
ResponderEliminarCada vez estará más interesante, porque ahora tendremos que utilizar todo, Álgebra, Geometría, Trigonometría, para poder entender y resolver Cálculo Diferencial e Integral.