Geometría: Ángulos

ÁNGULOS DETERMINADOS POR RECTAS PARALELAS CORTADAS POR UNA SECANTE

Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:

Las recta r corta a las rectas paralelas m y n:

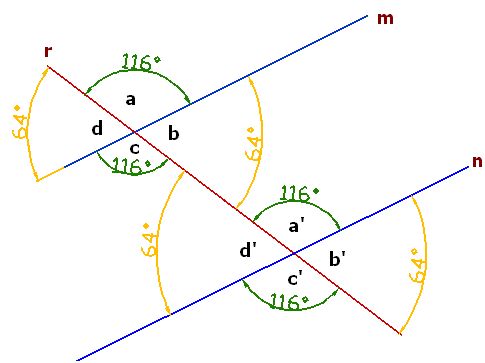
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:

Interiores o internos:

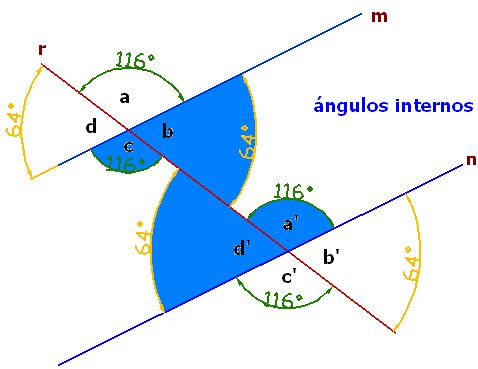
En azul, son los que se encuentran entre las rectas paralelas.

Ángulos exteriores o externos:

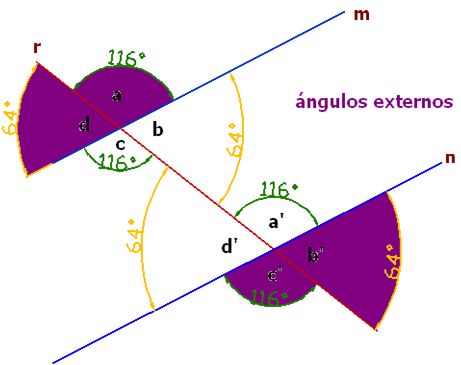
Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.

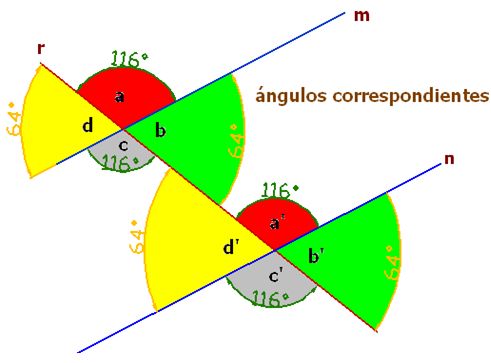
Ángulos correspondientes:

Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.

Los ángulos del mismo color son correspondientes:

El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’

Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.

Ángulos alternos internos

Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:

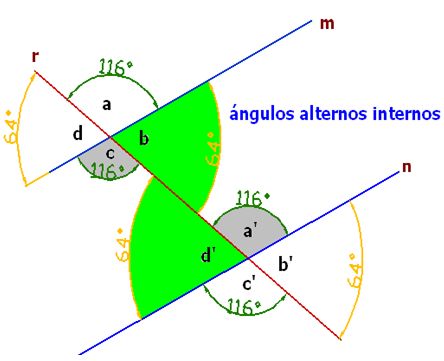
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.

 Ángulos alternos externos:

Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:

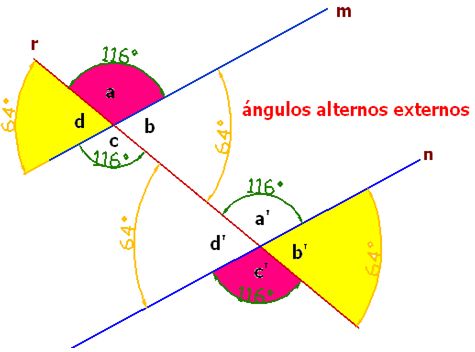
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.