LA PARIDAD DE UN OBJETO

En matemáticas, la  paridad  de un objeto indica si es par o impar.

Este concepto se inicia con números enteros. Un  número par  es un número entero que es "divisible" por 2, es decir, divisible por 2 y sin resto, un  número impar  es un entero que no es divisible por 2. (. El antiguo término "divisible" está ahora casi siempre abreviado como "divisible") Una definición formal de un número par es que es un número entero de la forma  n  = 2 k , donde  k  es un entero, sino que puede a continuación, se muestra que un número impar es un número entero de la forma  n  = 2 k  + 1.

Ejemplos de números pares son -4, 0, 8, y 1734. Ejemplos de números impares son -5, 3, 9, y 73. Esta clasificación se aplica sólo a números enteros, es decir, no enteros como 1/2 o 4,201 son ni siquiera ni impar.

Los conjuntos de números pares e impares se pueden definir de la siguiente manera:

Incluso  =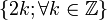 

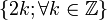
Odd  = 

Un número (es decir, entero) se expresa en el sistema de numeración decimal es par o impar, según su último dígito es par o impar. Es decir, si el último dígito es 1, 3, 5, 7, o 9, entonces es impar, de lo contrario es aún. La misma idea se trabajará utilizando cualquiera, incluso de base. En particular, un número expresado en el sistema de numeración binario es extraño que el último dígito es 1, e incluso si el último dígito es 0. En una base impar, el número es incluso de acuerdo con la suma de sus dígitos - es incluso si y sólo si la suma de sus dígitos es par.

ARITMÉTICAS CON NÚMEROS PARES E IMPARES.

Las siguientes leyes pueden ser verificados mediante las propiedades de divisibilidad. Ellos son un caso especial de las reglas en aritmética modular, y se utilizan comúnmente para comprobar si una igualdad es probable que sea correcta comprobando la paridad de cada lado. Al igual que con la aritmética ordinaria, multiplicación y la suma son conmutativa y asociativa, y la multiplicación es distributiva sobre la suma. Sin embargo, resta en la paridad es idéntica a la adición, por lo que resta también posee estas propiedades (que están ausentes de la aritmética ordinaria).

Suma y resta

• incluso ± = aunque aún;
• incluso ± impar = impar;
• ± impar impar = par;

Reglas análogas a éstas de divisibilidad por 9 se utilizan en el método de la expulsión de punta en blanco.

Multiplicación

• incluso × incluso = par;
• incluso × impar = par;
• × impar impar = impar.

División

La división de dos números enteros no se traduce necesariamente en un número entero. Por ejemplo, 1 dividido por 4 es igual a 1/4, que no es ni siquiera  ni  impar, ya que los conceptos par e impar se aplican sólo a números enteros. Pero cuando el cociente es un número entero, será incluso si y sólo si el dividendo tiene más factores de dos que el divisor.

HISTORIA. 

Los antiguos griegos consideraban 1 para ser ni completamente extraña, ni siquiera plenamente. Parte de este sentimiento sobrevivieron hasta el siglo 19: Friedrich Wilhelm August Fröbel 1826 La educación del hombre  indica al maestro para perforar a los estudiantes con la afirmación de que 1 es par ni impar, a la que se une la idea de último momento Fröbel filosófico.

Es así dirigir la atención del alumno aquí en vez de una gran ley de gran alcance de la naturaleza y del pensamiento. Es esta, la que existe entre dos cosas o ideas relativamente diferentes se alza siempre un tercero, en una especie de equilibrio, que parece unir a los dos. Por lo tanto, existe aquí entre los números pares e impares de un número (uno) que es ninguno de los dos. Del mismo modo, en la forma, el ángulo recto se interpone entre los ángulos agudos y obtusos, y en el lenguaje, las semi-vocales o aspirantes entre los mudos y vocales. Un profesor reflexivo y un alumno enseñado a pensar por sí mismo apenas puede evitar darse cuenta de esto y otras leyes importantes.

TEORÍA DE LA MÚSICA.

En los instrumentos de viento con agujero cilíndrico y en efecto cerrado en un extremo, como el clarinete en la boquilla, los armónicos producidos son múltiplos impares de la frecuencia fundamental. (Con tubos cilíndricos abiertos en ambos extremos, utilizados por ejemplo en algún órgano detiene tales como el diapasón abierta, los armónicos son múltiplos incluso de la misma frecuencia para la longitud de orificio dado, pero esto tiene el efecto de la frecuencia fundamental que se duplicó y todo múltiplos de esta frecuencia fundamental que se produce.) 

MATEMÁTICAS SUPERIORES.

Los números pares forman un ideal en el anillo de los números enteros, pero los números impares no lo hacen - esto es claro por el hecho de que el elemento de identidad para la suma, cero, es un elemento de las pares sólo números. Un entero es incluso si es congruente con 0 módulo este ideal, en otras palabras, si es congruente con 0 módulo 2, y si es impar es congruente con 1 módulo 2.

Todos los números primos son impares, con una excepción: el número primo 2. Todos los números perfectos conocidos son aún; se desconoce si existen números perfectos impares.

Los cuadrados de todos los números pares son iguales, y los cuadrados de todos los números impares son impares. Desde un número par se puede expresar como 2x, (2x) 2  = 4x 2  que es incluso.Desde un número impar se puede expresar como 2x + 1, (2x + 1) 2  = 4x 2  + 4x + 1. 4x 2  y 4x son aún, lo que significa que 4x 2  + 4x + 1 es impar (ya que incluso + impar = impar).

La conjetura de Goldbach afirma que cada entero par mayor que 2 se puede representar como una suma de dos números primos. Cálculos informáticos modernos han demostrado esta conjetura para ser cierto para los números enteros de hasta, al menos, 4 × 10 14 , pero todavía no se ha encontrado una prueba general.

El teorema Feit-Thompson afirma que un grupo finito siempre es solucionable si su orden es un número impar. Este es un ejemplo de los números impares que juegan un papel en un teorema matemático avanzado, donde el método de aplicación de la hipótesis simple de "orden impar" está lejos de ser evidente.

La venganza de Rubik en su estado resuelto

PARIDAD DE OTROS OBJETOS.

Paridad también se utiliza para referirse a una serie de otras propiedades.

• La paridad de una permutación (como se define en álgebra abstracta) es la paridad del número de transposiciones en el que la permutación se puede descomponer.Por ejemplo (ABC) a (BCA) es incluso porque se puede hacer mediante el canje de A y B a continuación, C y A (dos transposiciones). Se puede demostrar que ninguna de permutación se puede descomponer tanto en un par y en un número impar de transposiciones. Por lo tanto la anterior es una definición adecuada. En el Cubo de Rubik, Megaminx y otros rompecabezas de torsión, los movimientos del rompecabezas sólo permiten incluso permutaciones de las piezas del rompecabezas, por lo que la paridad es importante para comprender el espacio de configuración de estos puzzles.

• La paridad de una función se describe cómo sus valores cambian cuando sus argumentos se intercambian con sus negaciones. Una función par, como un poder aún de una variable, da el mismo resultado para cualquier argumento como por su negación. Una función impar, como una potencia impar de una variable, da para cualquier argumento de la negación de su resultado cuando se les da la negación de ese argumento. Es posible que una función sea ni extraña ni siquiera, y para el caso  f ( x ) = 0, al ser a la vez par e impar.

• Coordenadas enteras de puntos en espacios euclídeos de dos o más dimensiones también tienen una paridad, por lo general se define como la paridad de la suma de las coordenadas. Por ejemplo, la red de tablero de ajedrez contiene todos los puntos enteros de paridad par. Esta característica se manifiesta en el ajedrez, como obispos están obligados a plazas de la misma paridad; caballeros paridad alternan entre movimientos. Esta forma de la paridad fue célebremente usado para resolver el problema del tablero de ajedrez mutilado.