Aryabhata (476-550 dC) fue el primero en la línea de los grandes matemáticos-astrónomos de la época clásica de las matemáticas y la astronomía india indio. Sus trabajos incluyen el Aryabhatiya (499 CE, cuando tenía 23 años de edad) y la Arya-siddhanta.
Las obras de Aryabhata tratan principalmente las matemáticas y la astronomía. También trabajó en la aproximación de pi.

BIOGRAFÍA.
Si bien existe una tendencia a escribir mal su nombre como "Aryabhatta" por analogía con otros nombres que tienen el sufijo "bhatta", su nombre se escribe correctamente Aryabhata: todos los textos astronómicos deletrea su nombre por lo tanto, la inclusión de referencias de Brahmagupta para él "en más de una cientos de lugares por su nombre ". Por otra parte, en la mayoría de los casos "Aryabhatta" no encaja en el metro tampoco.
Aryabhata menciona en el Aryabhatiya que fue compuesto 3.600 años en el Kali Yuga, cuando tenía 23 años. Esto corresponde a 499 CE, e implica que él nació en el año 476.
Lugar de nacimiento del Aryabhata es incierto, pero podría haber estado en la zona conocida en los textos antiguos como Ashmaka la India, que pueden haber estado Maharashtra o Dhaka.
EDUCACIÓN.
Es casi seguro que, en algún momento, se fue a Kusumapura para estudios avanzados y vivió allí durante algún tiempo. Tanto la tradición hindú y budista, así como Bhāskara I (CE 629), identifican Kusumapura asPāṭaliputra, Patna moderna. Un verso menciona que Aryabhata fue el jefe de una institución ( kulapa ) en Kusumapura, y, porque la universidad de Nalanda fue en Pataliputra en el momento y tenía un observatorio astronómico, se especula que Aryabhata podría haber sido el jefe de la universidad de Nalanda así. Aryabhata también es conocido por haber creado un observatorio en el templo del Sol en Taregana, Bihar.

OTRAS HIPÓTESIS.
Alguna evidencia arqueológica sugiere que Aryabhata podría tener su origen en el día de hoy Kodungallur que fue la capital histórica de Thiruvanchikkulam de la antigua Kerala. Por ejemplo, una de las hipótesis era que Aśmaka (sánscrito para "piedra") puede ser la región de Kerala, que ahora se conoce como Koṭuṅṅallūr, basado en la creencia de que era conocido anteriormente como Koṭum-Kal-l-UR ("ciudad de disco piedras "), sin embargo, los registros antiguos muestran que la ciudad era en realidad Koṭum-kol-UR (" ciudad de la gobernanza estricta "). Del mismo modo, el hecho de que varios comentarios sobre el Aryabhatiya han venido de Kerala se utiliza para sugerir que era el lugar principal de Aryabhata de vida y actividad, sin embargo, muchos comentarios han venido de fuera de Kerala.
Aryabhata menciona "Lanka" en varias ocasiones en el Aryabhatiya , pero su "Lanka" es una abstracción, de pie para un punto en el ecuador de la misma longitud que su Ujjayini.
SISTEMA DE VALOR POSICIONAL Y EL CERO.
El sistema de valor, por primera vez en el siglo tercero Bakhshali Manuscrito, estaba claramente en su lugar en su obra. Mientras que él no utilizó un símbolo para el cero, el matemático francés Georges Ifrah argumenta que el conocimiento del cero estaba implícito en el sistema de valor posicional de Aryabhata como un marcador de posición para las potencias de diez, con nulos coeficientes.
Sin embargo, Aryabhata no utilizó los numerales Brahmi. Continuando con la tradición sánscrita de los tiempos védicos, utilizó las letras del alfabeto para designar números, expresando las cantidades, como la tabla de senos en forma mnemotécnica.

APROXIMACIÓN DE π
Aryabhata trabajó en la aproximación de pi (  ), y puede haber llegado a la conclusión de que
), y puede haber llegado a la conclusión de que  es irracional. En la segunda parte de la Aryabhatiyam (gaṇitapāda 10), escribe:
es irracional. En la segunda parte de la Aryabhatiyam (gaṇitapāda 10), escribe:
 ), y puede haber llegado a la conclusión de que
), y puede haber llegado a la conclusión de que  es irracional. En la segunda parte de la Aryabhatiyam (gaṇitapāda 10), escribe:
es irracional. En la segunda parte de la Aryabhatiyam (gaṇitapāda 10), escribe:caturadhikam śatamaṣṭaguṇam dvāṣaṣṭistathā Sahasranam
ayutadvayaviṣkambhasyāsanno vṛttapariṇāhaḥ."Agregar cuatro a 100, se multiplica por ocho, y luego añadir 62.000. Por esta regla de la circunferencia de un círculo con un diámetro de 20 000 puede ser abordado ".
Esto implica que la relación entre la circunferencia y el diámetro es ((4 + 100) × 8 + 62 000) / 20.000 = 62832/20000 = 3,1416, que tiene una precisión de cinco cifras significativas.
Se especula que Aryabhata usa la palabra āsanna (acercándose), en el sentido de que no sólo se trata de una aproximación, pero que el valor es inconmensurable (o irracional). Si esto es correcto, es bastante una visión sofisticada, ya que la irracionalidad de pi fue probado en Europa sólo en 1761 por Lambert.
Después Aryabhatiya fue traducido al árabe (c. 820 dC) esta aproximación fue mencionado en el libro de Al-Khwarizmi sobre álgebra.

TRIGONOMETRÍA.
En Ganitapada 6, Aryabhata da el área de un triángulo como se
- tribhujasya phalashariram samadalakoti bhujardhasamvargah
eso se traduce en: "para un triángulo, el resultado de una perpendicular con la cara medio es el área."
Aryabhata discutió el concepto de seno en su trabajo con el nombre de ardha-jya , que literalmente significa "medio-acordes". Para simplificar, la gente comenzó a llamarlo jya . Cuando los escritores árabes tradujeron sus obras de Sanskritinto árabe, se refirieron como jiba . Sin embargo, en los escritos árabes, las vocales se omiten, y se abrevian como jb . Escritores posteriores sustituidos con Jaib , que significa "bolsillo" o "veces (en una prenda de vestir)". (En árabe, jiba es una palabra sin sentido.) Más tarde, en el siglo 12, cuando Gherardo de Cremona tradujo estas escrituras del árabe al latín, reemplazó el árabe Jaib con su homólogo de América, del seno , lo que significa "cala" o "bahía" , de allí viene el Inglés sinusoidal .Código alfabético ha sido utilizado por él para definir una serie de incrementos. Si usamos la mesa del Aryabhata y calculamos el valor de sin (30) (correspondiente a hasjha) que es 1719/3438 = 0.5, el valor es correcto. Su código alfabético es conocido comúnmente como el sistema de cifrado Aryabhata.
ECUACIONES INDETERMINADAS.
Un problema de gran interés para los matemáticos de la India desde la antigüedad ha sido encontrar soluciones enteras de ecuaciones que tienen la forma ax + by = c, un tema que ha llegado a ser conocido como ecuaciones diofánticas. Este es un ejemplo de comentario de Bhāskara en Aryabhatiya:
- Encontrar el número que le da 5 como el resto cuando se divide por 8, 4 como el resto cuando se divide por 9, y 1 como el resto cuando se divide por 7
Es decir, encontrar N = 8x 5 = 9y 4 = 7z 1. Resulta que el valor más pequeño para N es 85. En general, las ecuaciones diofánticas, como ésta, pueden ser muy difíciles. Ellos fueron discutidos ampliamente en antiguos védicos textSulba Sutras, cuyas partes más antiguas podrían datar de 800 aC. Método de resolver este tipo de problemas de Aryabhata se llama la kuṭṭaka (कुट्टक) método. Kuttaka significa "pulverización" o "romper en trozos pequeños", y el método implica un algoritmo recursivo para la escritura de los factores originales en números más pequeños. Hoy este algoritmo, elaborado por Bhaskara en el 621 CE, es el método estándar para la resolución de ecuaciones diofánticas de primer orden y se refiere a menudo como el algoritmo de Aryabhata. Las ecuaciones diofánticas son de interés en la criptografía y la Conferencia RSA de 2006, se centró en la kuttaka método y trabajo previo en el Sulbasutras.
ÁLGEBRA.
En Aryabhatiya Aryabhata proporcionó resultados elegantes para la suma de una serie de cuadrados y cubos:
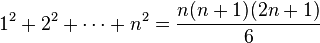
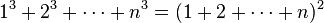
No hay comentarios:
Publicar un comentario