En la aritmética y el álgebra, el cubo de un número n es su tercer poder - el resultado del número multiplicado por sí mismo dos veces:
- n 3 = n × n × n .
Esta es también la fórmula del volumen de un cubo geométrico con lados de longitud N , dando lugar al nombre. La operación inversa de encontrar un número cuyo cubo es n se llama la extracción de la raíz cúbica de n . Se determina el lado del cubo de un volumen dado.También se n elevado a la tercera potencia de una sola.
El cubo de un número o cualquier otra expresión matemática se denota por un superíndice 3, por ejemplo 2 3 = 8 o ( x 1) 3 .
Un cubo perfecto (también llamado un número cubo , o, a veces sólo un cubo ) es un número que es el cubo de un número entero.
Los cubos perfectos positivos de hasta 60 3 son (secuencia A000578 en OEIS):
| 1 3 = 1 | 11 3 = 1331 | 21 3 = 9261 | 31 3 = 29,791 | 41 3 = 68,921 | 51 3 = 132,651 |
| 2 3 = 8 | 12 3 = 1728 | 22 3 = 10,648 | 32 3 = 32,768 | 42 3 = 74,088 | 52 3 = 140,608 |
| 3 3 = 27 | 13 3 = 2197 | 23 3 = 12,167 | 33 3 = 35,937 | 43 3 = 79,507 | 53 3 = 148,877 |
| 4 3 = 64 | 14 3 = 2744 | 24 3 = 13,824 | 34 3 = 39,304 | 44 3 = 85,184 | 54 3 = 157,464 |
| 5 3 = 125 | 15 3 = 3375 | 25 3 = 15,625 | 35 3 = 42,875 | 45 3 = 91,125 | 55 3 = 166,375 |
| 6 3 = 216 | 16 3 = 4096 | 26 3 = 17,576 | 36 3 = 46,656 | 46 3 = 97,336 | 56 3 = 175,616 |
| 7 3 = 343 | 17 3 = 4913 | 27 3 = 19,683 | 37 3 = 50 653 | 47 3 = 103,823 | 57 3 = 185,193 |
| 8 3 = 512 | 18 3 = 5832 | 28 3 = 21,952 | 38 3 = 54,872 | 48 3 = 110,592 | 58 3 = 195,112 |
| 9 3 = 729 | 19 3 = 6859 | 29 3 = 24,389 | 39 3 = 59,319 | 49 3 = 117,649 | 59 3 = 205,379 |
| 10 3 = 1000 | 20 3 = 8000 | 30 3 = 27,000 | 40 3 = 64,000 | 50 3 = 125,000 | 60 3 = 216,000 |
Geométricamente hablando, un número positivo m es un cubo perfecto si y sólo si se puede organizar m unidades de cubos sólidos en una, cubo sólido más grande. Por ejemplo, 27 pequeños cubos se pueden organizar en un uno más grande con la apariencia de un cubo de Rubik, desde el 3 × 3 × 3 = 27.
El patrón entre cada cubo perfecto desde menos infinito a más infinito es el siguiente,
N 3 = ( n - 1) 3 + 3 ( n - 1) n + 1.
o
N 3 = ( n + 1) 3 - 3 ( n + 1) n - 1.
CUBOS EN TEORÍA DE NÚMEROS.
No hay cubo perfecto más pequeño, ya que se incluyen los números enteros negativos. Por ejemplo, (-4) × (-4) × (-4) = -64. Para cualquier n , (- n ) 3 = - ( n 3 ).
BASE DE DIEZ.
A diferencia de cuadrados perfectos, cubos perfectos no tienen un pequeño número de posibilidades para los dos últimos dígitos. Excepto para los cubos divisibles por 5, donde sólo el 25 , 75 y 00 pueden ser los dos últimos dígitos, cualquier par de dígitos con el último dígito impar puede ser un cubo perfecto. Incluso con los cubos, hay restricción considerable, pues sólo 00 , o2 , e4 , o6 y e8 pueden ser los dos últimos dígitos de un cubo perfecto (donde o representa cualquier dígito impar y e incluso para cualquier dígito). Algunos números del cubo son también números cuadrados, por ejemplo, 64 es un número cuadrado (8 × 8) y un número del cubo (4 × 4 × 4), lo que sucede si y sólo si el número es un sexto poder perfecto.
Es, sin embargo, fácil de demostrar que la mayoría de los números no son cubos perfectos porque todos los cubos perfectos deben tener raíz digital de 1 , 8 o 9 . Por otra parte, la raíz digital del cubo de cualquier número puede ser determinado por el resto del número da cuando se divide por 3:
- Si el número es divisible por 3, el cubo tiene raíz digital de 9;
- Si tiene un resto de 1 cuando se divide por 3, su cubo tiene raíz digital de 1;
- Si tiene un resto de 2 cuando se divide por 3, su cubo tiene raíz digital de 8.
EL PROBLEMA DE WARING DURANTE CUBOS.
Cada número entero positivo puede escribirse como la suma de nueve (o menos) cubos positivos. Este límite superior de nueve cubos no se puede reducir porque, por ejemplo, 23 no se puede escribir como la suma de menos de nueve cubos positivos:
- 23 = 2 3 2 + 3 + 1 3 + 1 3 + 1 3 + 1 3 + 1 3 + 1 3 + 1 3 .
EL ÚLTIMO TEOREMA DE FERMAT PARA LOS CUBOS.
La ecuación x 3 + y 3 = z 3 no tiene no triviales (es decir xyz ≠ 0) soluciones en números enteros. De hecho, no tiene ninguno de los enteros de Eisenstein.
Ambas declaraciones son también cierto para la ecuación x 3 + y 3 = 3 z 3 .
SUMAS DE CUBOS RACIONALES.
Cada número racional positivo es la suma de tres cubos racionales positivos, y no son racionales que no son la suma de dos cubos racionales.
Suma de primera n cubos
La suma de los primeros n cubos es el N º número de triángulo cuadrado:
Por ejemplo, la suma de los primeros 5 cubos es el cuadrado de la quinta número triangular,
Un resultado similar se puede dar por la suma de los primeros Y cubos impares,
pero { x, y } debe satisfacer la ecuación de Pell negativo 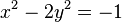 . Por ejemplo, para y = 5 y 29, a continuación,
. Por ejemplo, para y = 5 y 29, a continuación,
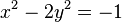 . Por ejemplo, para y = 5 y 29, a continuación,
. Por ejemplo, para y = 5 y 29, a continuación,
y así sucesivamente. Además, cada número par perfecto, excepto el primero, es la suma de la primera 2 ( p -1) / 2 cubos impares,
Suma de cubos en progresión aritmética
Hay ejemplos de cubos en progresión aritmética cuya suma es un cubo,
con el primero también conocido como número de Platón. La fórmula F para encontrar la suma de un n número de cubos en progresión aritmética con diferencia común d y el cubo inicial un 3 ,
está dada por,
Una solución paramétrica para,
se conoce para el caso especial de d = 1, o cubos consecutivos, pero sólo las soluciones esporádicos son conocidos por entero d > 1, tal como d = 2, 3, 5, 7, 11, 13, 37, 39, etc
HISTORIA.
Determinación de los cubos de un gran número era muy común en muchas civilizaciones antiguas. Aryabhata, el antiguo matemático indio en su famosa obra Aryabhatiya explica el significado matemático de cubo (Aryabhatiya, 2-3), como "el producto continua de tres es igual a como también el (rectangular) sólido que tiene 12 aristas iguales se llaman cubo". Definiciones similares se pueden observar en los textos antiguos como Brahmasphuta Siddhanta (xviii. 42), Ganitha sara sangraha (II. 43) y Siddhanta Sekhara (xiii. 4). Es interesante que en las matemáticas modernas también, el término "Cube" es sinónimo de dos significados matemáticos al igual que en sánscrito, donde la palabra Ghhana significa un factor de potencia con el número, multiplicado por sí mismo tres veces y también una estructura cúbica.En 2010 Alberto Zanoni encontrado un nuevo algoritmo para calcular el cubo de un entero largo de un cierto rango, más rápido que la cuadratura y de multiplicación.

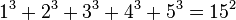

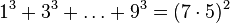

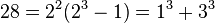


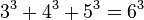




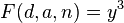
No hay comentarios:
Publicar un comentario