Arquímedes de Siracusa (griego: Ἀρχιμήδης; . c 287 BC - . c 212 aC) fue un matemático griego, físico, ingeniero, inventor y astrónomo.Aunque se conocen pocos detalles de su vida, es considerado como uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física son los fundamentos de la hidrostática, staticsand una explicación del principio de la palanca. Se le atribuye el diseño de máquinas innovadoras, incluyendo los motores del cerco y la bomba de tornillo que lleva su nombre. Los experimentos modernos han probado demandas que Arquímedes máquinas capaces de levantar atacar a los barcos fuera del agua y de fijar las naves en el fuego usando un arsenal de espejos diseñados.
Arquímedes es generalmente considerado como el más grande matemático de la antigüedad y uno de los más grandes de todos los tiempos. Usó el método de agotamiento para calcular el área bajo el arco de una parábola con la suma de una serie infinita, y dio una aproximación notablemente exacta de pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy grandes.
Arquímedes murió durante el sitio de Siracusa cuando fue asesinado por un soldado romano a pesar de las órdenes que él no debe ser dañado. Cicerón describe visitar la tumba de Arquímedes, que fue coronada por una esfera inscrita dentro de un cilindro. Arquímedes había demostrado que la esfera tiene dos tercios de la superficie de volumen y superficie del cilindro (incluyendo las bases de este último), y considera esto como el mayor de sus logros matemáticos.
A diferencia de sus inventos, los escritos matemáticos de Arquímedes eran poco conocidas en la antigüedad. Los matemáticos de Alejandría leído y citado a él, pero la primera recopilación completa no se hizo hasta c. 530 dC por Isidoro de Mileto, mientras que los comentarios sobre los trabajos de Arquímedes escritos por Eutocio en el siglo VI dC los abrieron a mayor número de lectores por primera vez . Las relativamente pocas copias de trabajos escritos de Arquímedes que sobrevivieron a través de la Edad Media fueron una fuente de influencia de las ideas de los científicos durante el Renacimiento, [6] mientras que el descubrimiento en 1906 de las obras hasta ahora desconocidas por Arquímedes en el Palimpsesto de Arquímedes ha proporcionado nuevos conocimientos sobre cómo obtuvo resultados matemáticos.
Esta estatua de bronce de Arquímedes es en el Observatorio Archenhold en Berlín. Fue esculpida por Gerhard Thieme y dio a conocer en 1972.
BIOGRAFÍA.
Arquímedes nació c .287 aC en la ciudad puerto de Siracusa, Sicilia, en ese momento una colonia autónoma en la Magna Grecia. La fecha de nacimiento se basa en una declaración del historiador griego bizantino Juan Tzetzes que Arquímedes vivió durante 75 años. [8] En El contador de arena , Arquímedes da el nombre de su padre como Fidias, un astronomerabout quien no se sabe nada. Plutarco escribió en sus Vidas paralelas que Arquímedes estaba relacionado con el rey Hierón II, el gobernante de Siracusa. Una biografía de Arquímedes fue escrito por su amigo Heráclides pero este trabajo se ha perdido, dejando los detalles de su vida oscura. No se sabe, por ejemplo, si alguna vez se casó ni tuvo hijos. Durante su juventud, Arquímedes pudo haber estudiado en Alejandría, Egipto, donde Conon de Samos y Eratóstenes de Cirene fueron contemporáneos. Se refirió a Conon de Samos como su amigo, mientras que dos de sus obras ( El método de los teoremas mecánicos y el Problema del ganado ) han introducciones dirigidas a Eratóstenes.
Arquímedes murió c . 212 aC durante la Segunda Guerra Púnica, cuando las fuerzas romanas al mando del general Marco Claudio Marcelo capturaron la ciudad de Siracusa después de dos años de largo asedio. Según el relato popular dada por Plutarco, Arquímedes estaba contemplando un diagrama matemático en que se capturó la ciudad. Un soldado romano le ordenó venir y conocer a Marcelo generales pero se negó, diciendo que tenía que terminar de trabajar en el problema. El soldado se enfureció por este, y Arquímedes con su espada mató. Plutarco también ofrece un relato menos conocido de la muerte de Arquímedes que sugiere que pudo haber sido asesinado mientras intentaba rendirse a un soldado romano. Según esta historia, Arquímedes fue llevando instrumentos matemáticos, y fue asesinado porque el soldado pensó que eran objetos de valor. Según los informes general Marcellus estaba enojado por la muerte de Arquímedes, como él le un activo de gran valor científico examinó y ordenó que no se vea perjudicada.
Las últimas palabras atribuidas a Arquímedes son de "No molestar mis círculos" (griego: μή μου τοὺς κύκλους τάραττε), una referencia a los círculos en el dibujo matemático que supuestamente estaba estudiando cuando son perturbados por el soldado romano. Esta cita se da a menudo en latín como "Noli turbare circulos meos", pero no hay evidencia confiable de que Arquímedes pronunció estas palabras y que no aparecen en el relato de Plutarco.
La tumba de Arquímedes realizó una escultura que ilustra su prueba matemática favorita, que consiste en una esfera y un cilindro de la misma altura y diámetro. Arquímedes habían demostrado que el volumen y área de superficie de la esfera son dos tercios la del cilindro incluyendo sus bases. En el año 75 aC, 137 años después de su muerte, el orador romano Cicerón estaba sirviendo como cuestor en Sicilia. Había oído historias sobre la tumba de Arquímedes, pero ninguno de los locales fue capaz de darle la ubicación. Finalmente encontró la tumba cerca de la puerta de Agrigento en Siracusa, en una condición de abandonado y cubierto de arbustos. Cicerón tenía la tumba limpia, y era capaz de ver la talla y leer algunos de los versos que se habían añadido como una inscripción. Una tumba descubierta en un patio del hotel en Siracusa, en la década de 1960 se afirma que es la de Arquímedes, pero su ubicación actual es desconocida.
Las versiones estándar de la vida de Arquímedes fueron escritos mucho después de su muerte por los historiadores de la antigua Roma. El relato del asedio de Siracusa dado byPolybius en su Historia universal fue escrito alrededor de setenta años después de la muerte de Arquímedes, y fue utilizado posteriormente como fuente de Plutarco y Tito Livio. Arroja algo de luz sobre Arquímedes como persona, y se centra en las máquinas de guerra que se dice que ha construido para defender la ciudad.
DESCUBRIMIENTOS E INVENSIONES.
Arquímedes pudo haber utilizado su principio de flotabilidad para determinar si la corona de oro era menos denso que el oro sólido.
El principio de Arquímedes
La anécdota más conocida sobre Arquímedes cuenta cómo inventó un método para determinar el volumen de un objeto con una forma irregular. Según toVitruvius, una corona votiva de un templo se había hecho para el rey Hierón II, que había suministrado el oro puro para ser utilizado, y Arquímedes se le preguntó para determinar si alguna silverhad sido sustituido por el deshonesto orfebre.Arquímedes tenía que resolver el problema sin dañar la corona, así que no podía fundirla en un cuerpo en forma regular con el fin de calcular su densidad. Al tiempo que toma un baño, se dio cuenta de que el nivel del agua en la bañera rosa como él entró, y se dio cuenta de que este efecto podría ser utilizado para determinar el volumen de la corona. Para fines prácticos agua es incompresible, por lo que la corona sumergida desplazaría una cantidad de agua igual a su propio volumen. Al dividir la masa de la corona por el volumen de agua desplazada, la densidad de la corona podría ser obtenida. Esta densidad sería menor que la de oro si se habían añadido metales más baratos y menos densos. Arquímedes luego salió a la calle desnudo, tan emocionado por su descubrimiento de que se había olvidado de vestirse, gritando "¡Eureka!" (Griego: "¡Lo he encontrado!" "Εὕρηκα", es decir). La prueba se llevó a cabo con éxito, lo que demuestra que la plata de hecho había sido mezclado pulg
La historia de la corona dorada no aparece en los trabajos conocidos de Arquímedes. Por otra parte, el sentido práctico del método que describe se ha puesto en duda, debido a la extrema precisión con la que se tendría que medir el desplazamiento de agua. Arquímedes pueden tener lugar buscó una solución que aplica el principio conocido inhydrostatics como el principio de Arquímedes, que él describe en su tratado Sobre los cuerpos flotantes . Este principio establece que todo cuerpo sumergido en un fluido experimenta un forceequal boyante al peso del fluido que desaloja. Utilizando este principio, habría sido posible comparar la densidad de la corona de oro a la de oro sólido mediante el equilibrio de la corona en una escala con una muestra de referencia de oro, a continuación, sumergir el aparato en agua. La diferencia de densidad entre las dos muestras causaría la escala a la punta en consecuencia. Galileo consideró "probable que este método es el mismo que Arquímedes siguió, ya que, además de ser muy preciso, que se basa en las manifestaciones que se encuentran por el propio Arquímedes." En un texto del siglo 12 titulado Mappae clavícula hay instrucciones sobre cómo realizar la pesadas en el agua con el fin de calcular el porcentaje de plata utilizada, y por lo tanto resolver el problema. El poema latino Carmen de ponderibus et mensuris del cuarto o quinto siglo describe el uso de una balanza hidrostática para resolver el problema de la corona, y atribuye el método de Arquímedes.
Tornillo de Arquímedes
Una gran parte del trabajo de Arquímedes en la ingeniería surgió de satisfacer las necesidades de su ciudad natal de Siracusa. El escritor griego Ateneo de Naucratis describe cómo el rey Hierón II encargó a Arquímedes para diseñar un barco enorme, el Syracusia , que podría ser utilizado para los viajes de lujo, con suministros, y, como un buque de guerra naval. El Syracusia se dice que ha sido el barco más grande construido en la antigüedad clásica. Según Ateneo, era capaz de transportar a 600 personas e incluyó decoraciones de jardín, agymnasium y un templo dedicado a la diosa Afrodita en sus instalaciones. Dado que un barco de este tamaño se filtraría una cantidad considerable de agua a través del casco, tornillo theArchimedes fue desarrollado supuestamente con el fin de eliminar el agua de sentina. Máquina de Arquímedes era un dispositivo con una cuchilla en forma de tornillo que gira dentro de un cilindro. Se volvió a mano, y también se podría utilizar para transferir agua de un cuerpo de baja altitud de agua en los canales de riego. El tornillo de Arquímedes se encuentra todavía en uso hoy en día para bombear líquidos y sólidos granulados tales como carbón y cereales. El tornillo de Arquímedes se describe en la época romana por Vitruvio puede haber sido una mejora con respecto a una bomba de tornillo que se utilizó para el riego de los jardines colgantes de Babilonia. Primer buque de vapor de alta mar del mundo con una hélice fue el SS de Arquímedes , que fue lanzado en 1839 y nombrado en honor de Arquímedes y su trabajo en el tornillo.
Garra de Arquímedes
La garra de Arquímedes es un arma que se dice que ha diseñado con el fin de defender la ciudad de Siracusa. También conocido como "el agitador de la nave", la garra consistía en un brazo-grúa como de la que fue suspendido un gancho de metal. Cuando la uña se dejó caer en una nave atacante del brazo puede dar vuelta hacia arriba, levantando el barco fuera del agua y, posiblemente, hundiéndolo. Se han realizado experimentos modernos para poner a prueba la viabilidad de la garra, y en 2005 un documental de televisión titulado Superarmas del mundo antiguo construido una versión de la garra y la conclusión de que se trataba de un dispositivo viable.
Arquímedes pudo haber utilizado espejos actúan en conjunto como un reflector parabólico para quemar naves atacantes Syracuse.
Rayo de calor
El segundo siglo de nuestra era autor Lucian escribió que durante el sitio de Siracusa ( c. 214-212 aC), Arquímedes destruyó las naves enemigas con fuego.Siglos más tarde, Antemio de Tralles menciona la quema de las gafas como arma de Arquímedes. El dispositivo, llamado a veces el "rayo de calor de Arquímedes", se utiliza para enfocar la luz solar en acercarse a los barcos, haciendo que se prenda fuego.
Esta supuesta arma ha sido el tema de debate en curso acerca de su credibilidad desde el Renacimiento. René Descartes rechazó como falsa, mientras que los investigadores modernos han intentado recrear el efecto utilizando sólo los medios que habrían estado a disposición de Arquímedes. Se ha sugerido que una gran variedad de bronce o cobre escudos altamente pulidos que actúan como espejos podrían haber sido empleados para enfocar la luz solar en un barco. Esto habría utilizado el principio del reflector parabólico de una manera similar a un horno solar.
Una prueba del rayo de calor de Arquímedes se llevó a cabo en 1973 por el científico griego Ioannis Sakkas. El experimento se llevó a cabo en las Skaramagas outsideAthens base naval. En esta ocasión se utilizaron 70 espejos, cada uno con un recubrimiento de cobre y un tamaño de alrededor de cinco por tres pies (1,5 por 1 m). Los espejos fueron señalados en una plywoodmock en marcha de un buque de guerra romano a una distancia de alrededor de 160 pies (50 m). Cuando los espejos estaban enfocados con precisión, la nave estalló en llamas en cuestión de segundos. El barco de madera contrachapada tenía un recubrimiento de pintura de alquitrán, que puede haber ayudado de combustión. Una capa de alquitrán habría sido un lugar común en los barcos en la época clásica.
En octubre de 2005 un grupo de estudiantes del Instituto de Tecnología de Massachusetts llevó a cabo un experimento con 127 de un pie (30 cm) azulejos cuadrados de espejos, se centró en el barco de madera amock-up en un rango de alrededor de 100 pies (30 m). Las llamas estallaron en una corrección de la nave, pero sólo después de que el cielo había estado despejado y la nave había permanecido estacionaria durante unos diez minutos. Se concluyó que el dispositivo era un arma viable bajo estas condiciones. El grupo del MIT repitió el experimento para el programa de televisión MythBusters , usando un barco de pesca de madera en San Francisco como destino. De nuevo se produjo algo de carbonización, junto con una pequeña cantidad de la llama.Con el fin de coger el fuego, la madera necesita para alcanzar su temperatura de autoignición, que es de alrededor de 300 ° C (570 ° F).
Cuando MythBusters difundió el resultado del experimento de San Francisco en enero de 2006, la reclamación fue colocado en la categoría de "roto" (o no) a causa de la cantidad de tiempo y de las condiciones climáticas ideales requeridas para la combustión que se produzca. También se señaló que desde Syracuse mira al mar, hacia el este, la flota romana habría tenido que atacar durante la mañana para la recolección óptima de la luz por los espejos. MythBusters también señaló que el armamento convencional, como flechas incendiarias o pernos de una catapulta, habría sido una manera mucho más fácil de crear un barco en llamas en las distancias cortas.
En diciembre de 2010, MythBusters de nuevo miró a la historia rayo de calor en una edición especial con Barack Obama, titulado Desafío del Presidente . Varios experimentos se llevaron a cabo, incluyendo una prueba a gran escala con 500 niños en edad escolar con el objetivo espejos en una maqueta de un barco de vela romana 400 pies (120 m) de distancia. En todos los experimentos, la vela no logró alcanzar los 210 ° C (410 ° F) necesario para coger el fuego, y el veredicto fue de nuevo "reventado". El espectáculo concluyó que un efecto más probable de los espejos se habría cegadora y deslumbrante, o distraer a la tripulación de la nave.
Otros descubrimientos e invenciones
Mientras que Arquímedes no inventó la palanca, dio una explicación del principio implicado en su trabajo En el equilibrio de los planos .Descripciones anteriores de la palanca se encuentran en la escuela peripatética de los seguidores de Aristóteles, y, a veces se atribuyen a Arquitas. Según Pappus de Alejandría, el trabajo de Arquímedes sobre palancas le hizo una observación: "Dadme un punto de apoyo y moveré la tierra." (Griego: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω) Plutarco describe cómo Arquímedes diseñados cuadra y abordar sistemas de poleas, lo que permite a los navegantes utilizan el principio de la palanca para levantar objetos que de otro modo habrían sido demasiado pesados para moverlos. Arquímedes también se ha acreditado con la mejora de la potencia y la precisión de la catapulta, y la invención del odómetro durante la Primera Guerra Púnica. El odómetro fue descrito como un carro con un mecanismo de engranaje que dejó caer una pelota en un contenedor después de cada milla recorrida.
Cicerón (106-43 aC) menciona brevemente Arquímedes en su diálogo De re publica , que retrata una conversación ficticia que tiene lugar en 129 antes de Cristo. Tras la captura de Siracusa c. 212 aC, se dijo el general Marco Claudio Marcelo haber llevado de vuelta a Roma dos mecanismos, construidos por Arquímedes y utilizadas como coadyuvantes de la astronomía, que mostraron el movimiento del Sol, la Luna y cinco planetas. Cicerón menciona mecanismos similares diseñados por Tales de Mileto y Eudoxo de Cnido. El diálogo dice que Marcelo se quedó con uno de los dispositivos como su único botín personal de Siracusa, y donó el otro para el Templo de la Virtud en Roma. Marcellus mecanismo 'se demostró, según Cicerón, por Cayo Sulpicio Gallus a Lucio Furio Filo, quien lo describió así:
Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus en aere illo quot Diebus en ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum en eam metam quae ESSET terrae umbra, sol cum e regione . - Cuando Gallus trasladó el mundo, sucedió que la Luna sigue el Sol por el mayor número de vueltas en ese artilugio de bronce como en el mismo cielo, de donde también en el cielo globo del Sol se convirtió en tener ese mismo eclipse, y la Luna llegó a continuación, a esa posición, que era su sombra sobre la Tierra, cuando el Sol estaba en línea.
Esta es una descripción de un planetario o planetario. Pappus de Alejandría dijo que Arquímedes había escrito un manuscrito (ahora perdido) en la construcción de estos mecanismos titulado Sobre hacer esferas . La investigación moderna en esta área se ha centrado en el mecanismo de Antikythera, otro dispositivo de la antigüedad clásica que probablemente fue diseñado para el mismo propósito. La construcción de mecanismos de este tipo habría requerido un conocimiento sofisticado de engranaje diferencial. Esta vez se pensó que fue más allá del alcance de la tecnología disponible en la antigüedad, pero el descubrimiento del mecanismo de Antikythera en 1902 ha confirmado que los dispositivos de este tipo eran conocidos por los antiguos griegos.
Como demostrado por Arquímedes, el área del segmento parabólico en la figura superior es igual a 43 que del triángulo inscrito en la figura inferior.
MATEMÁTICAS.
Mientras que él es a menudo considerado como un diseñador de dispositivos mecánicos, Arquímedes también hizo contribuciones en el campo de las matemáticas. Plutarco escribió: "Él puso todo su afecto y ambición en esas especulaciones más puras en donde no puede haber una referencia a las necesidades vulgares de la vida."
Arquímedes fue capaz de utilizar los infinitesimales de una manera que es similar al cálculo integral moderna. A través de la prueba por la contradicción (reducción al absurdo), podría dar respuestas a los problemas en un grado arbitrario de precisión, especificando los límites en los que la respuesta estaba. Esta técnica se conoce como el método de agotamiento, y se servía de él para aproximar el valor de π.En Medición de un círculo que hizo esta dibujando un hexágono regular más grande fuera de un círculo y un hexágono regular más pequeño dentro del círculo, y duplicando progresivamente el número de lados de cada polígono regular, el cálculo de la longitud de un lado de cada polígono en cada paso . Como el número de lados aumenta, se convierte en una aproximación más exacta de un círculo. Después de cuatro de estos pasos, cuando los polígonos tenían 96 lados cada uno, él fue capaz de determinar que el valor de π se extendía entre 3 1 / 7 (aproximadamente 3,1429) y 3 10 / 71 (aproximadamente 3,1408), de acuerdo con su valor actual de aproximadamente 3.1416. También demostró que thearea de un círculo era igual a π multiplicado por el cuadrado del radio del círculo (πr 2 ). En Sobre la esfera y el cilindro , de Arquímedes postula que cualquier magnitud cuando se añade a sí mismo suficientes veces superará cualquier magnitud dada. Esta es la propiedad de Arquímedes de los números reales.
En Medida de un Círculo , Arquímedes da el valor de la raíz cuadrada de 3, como se extiende entre 265 / 153 (aproximadamente 1,7320261) y 1351 / 780 (aproximadamente 1,7320512). El valor real es aproximadamente 1.7320508, haciendo de esta una estimación muy precisa. Se presentó este resultado sin ofrecer ninguna explicación de cómo había conseguido. Este aspecto de la obra de Arquímedes causado John Wallis para comentar que él era: "como si fuera de propósito fijo haber cubierto las huellas de su investigación como si se hubiera escatimado posteridad el secreto de su método de investigación, mientras que él deseaba para extorsionar de ellos asentimiento a sus resultados. "Es posible que él utilizó un iterativeprocedure para calcular estos valores.
En La cuadratura de la parábola , Arquímedes demostró que el área encerrada por una parábola y una línea recta es 4 / 3 veces el área de un triangleas correspondientes inscripciones que aparecen en la figura de la derecha. Expresó la solución al problema como una serie geométrica infinita con la razón común de 1 / 4 :
Si el primer término en esta serie es el área del triángulo, a continuación, la segunda es la suma de las áreas de dos triángulos cuyas bases son las dos líneas secantes más pequeños, y así sucesivamente. Esta prueba utiliza una variación de la serie 1/4 + 1/16 + 1/64 + 1/256 + · · · que resume a 1 / 3 .
En El contador de arena , Arquímedes se dispuso a calcular el número de granos de arena que el universo podría contener. Al hacerlo, él desafió la noción de que el número de granos de arena era demasiado grande como para ser contados. Él escribió: "Hay algunos, Rey Gelo (Gelo II, hijo de Hierón II), que piensan que el número de la arena es infinito en multitud; y lo digo por la arena, no sólo lo que existe alrededor de Siracusa y el resto de Sicilia, sino también la que se encuentra en todas las regiones habitadas o deshabitadas si. "Para resolver el problema, Arquímedes ideó un sistema de recuento basado en la miríada. La palabra es de la μυριάς griega Murias , para el número 10000. Propuso un sistema de numeración que utilizan potencias de una miríada de miríadas (100 millones) y llegó a la conclusión de que el número de granos de arena necesarios para llenar el universo sería 8vigintillion u 8 × 10 63 .
LEGACY
Hay un cráter en la Luna llamado Arquímedes (29.7 ° N, 4.0 ° W) en su honor, así como una cordillera lunar, los Montes de Arquímedes (25.3 ° N, 4.6 ° W).
El asteroide 3600 lleva el nombre de Arquímedes él.
La Medalla Fields por logros sobresalientes en matemáticas lleva un retrato de Arquímedes, junto con una talla que ilustra su prueba sobre la esfera y el cilindro. La inscripción en la cabeza de Arquímedes es una cita atribuida a él, que dice en latín: "Transire suum pectus mundoque potiri" (Elévate por encima de uno mismo y comprender el mundo).
Arquímedes ha aparecido en los sellos postales emitidos por Alemania Oriental (1973), Grecia (1983), Italia (1983), Nicaragua (1971), San Marino (1982) y España (1963).
La exclamación de ¡Eureka! atribuida a Arquímedes es el lema del estado de California. En este caso, la palabra se refiere al descubrimiento de oro cerca de Molino de Sutter en 1848 que desató la fiebre del oro de California.
Un movimiento para la participación cívica dirigida a un acceso universal a servicios de salud en el estado de Oregon EE.UU. ha sido nombrado el "Movimiento de Arquímedes", encabezada por el ex gobernador de Oregón John Kitzhaber.
El asteroide 3600 lleva el nombre de Arquímedes él.
La Medalla Fields por logros sobresalientes en matemáticas lleva un retrato de Arquímedes, junto con una talla que ilustra su prueba sobre la esfera y el cilindro. La inscripción en la cabeza de Arquímedes es una cita atribuida a él, que dice en latín: "Transire suum pectus mundoque potiri" (Elévate por encima de uno mismo y comprender el mundo).
Arquímedes ha aparecido en los sellos postales emitidos por Alemania Oriental (1973), Grecia (1983), Italia (1983), Nicaragua (1971), San Marino (1982) y España (1963).
La exclamación de ¡Eureka! atribuida a Arquímedes es el lema del estado de California. En este caso, la palabra se refiere al descubrimiento de oro cerca de Molino de Sutter en 1848 que desató la fiebre del oro de California.
Un movimiento para la participación cívica dirigida a un acceso universal a servicios de salud en el estado de Oregon EE.UU. ha sido nombrado el "Movimiento de Arquímedes", encabezada por el ex gobernador de Oregón John Kitzhaber.





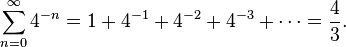

No hay comentarios:
Publicar un comentario