OLOID

Un  oloid  es un objeto geométrico curva tridimensional que fue descubierto por Paul Schatz en 1929. Es el casco convexo de un bastidor de esqueleto hecho mediante la colocación de dos círculos congruentes con enlaces en planos perpendiculares, de modo que el centro de cada círculo se encuentra en el otro círculo. La distancia entre los centros de círculo es igual al radio de los círculos. Una tercera parte de 'el perímetro de cada círculo se encuentra en el interior de la envolvente convexa, por lo que la misma forma también se puede formar como la envolvente convexa de los dos restantes arcos circulares cada abarcan un ángulo de 2π / 3.

Superficie y volumen

El área de superficie de un oloid está dada por:

exactamente el mismo que el área de superficie de una esfera con el mismo radio. En forma cerrada, el volumen encerrado es

,

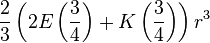donde  K  y  E  designan las integrales elípticas completas del primero y segundo tipo respectivamente. Un cálculo numérico da:

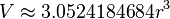
Cinética

La superficie de la oloid es una superficie desarrollable, lo que significa que los parches de la superficie pueden aplanado en un plano. Si bien rodando, desarrolla toda su superficie: cada punto de la oloid toca el plano en el que se está rodando, en algún momento durante el movimiento de balanceo. A diferencia de la mayoría de los objetos simétricos axiales (cilindro, esfera, etc), mientras que rueda sobre una superficie plana, su centro de massperforms un movimiento de meandro en lugar de uno lineal. En cada ciclo de rodadura, la distancia entre el centro de la oloid de la masa y la superficie de rodadura tiene dos mínimos y dos máximos. La diferencia entre el máximo y la altura mínima viene dada por:

Donde  R  es circular radio de los arcos de la oloid. Dado que esta diferencia es bastante pequeña, movimiento de balanceo de la oloid es relativamente lisa.

En cada punto durante este movimiento de balanceo, el oloid toca el avión en un segmento de línea. La longitud de este segmento se mantiene sin cambios durante todo el movimiento, y está dada por:

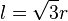
Formas relacionadas

El sphericon es la envolvente convexa de dos semicírculos en planos perpendiculares, con centros en un solo punto. Su superficie se compone de las piezas de cuatro conos. Se asemeja a la oloid en forma y, como él, es la superficie adevelopable que puede ser desarrollada por laminación. Sin embargo, su ecuador es un cuadrado con cuatro esquinas agudas, a diferencia de la oloid que no tiene esquinas agudas.

Otro objeto de la llama de dos rodillos círculo se define a partir de dos círculos perpendiculares para los que la distancia entre sus centros se √ 2 veces su radio, más separados que la oloid. O bien se puede formar (como el oloid) como la envolvente convexa de los círculos, o mediante el uso de sólo los dos discos delimitadas por los dos círculos. A diferencia de la oloid su centro de gravedad se mantiene a una distancia constante desde el suelo, para que ruede más suavemente que la oloid.