Dados Sicherman son el único par de dados de 6 lados que no son dados normales, soportar sólo enteros positivos, y tienen la misma distribución de probabilidad de la suma como dados normales.
Las caras de los dados están numerados 1, 2, 2, 3, 3, 4 y 1, 3, 4, 5, 6, 8.
Matemáticas
Dados Loco es un problema matemático estándar o rompecabezas en combinatoria elemental, que implica una re-etiquetado de las caras de un par de dados de seis caras para reproducir la misma frecuencia de las cantidades que el etiquetado estándar.
Es un ejercicio estándar en combinatoria elementales para calcular el número de formas de rodadura cualquier valor dado con un par de dados equilibrados de seis caras (tomando la suma de los dos rodillos). La tabla muestra el número de tales formas de rodar un valor dado 
:
:| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| # De maneras | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 |
Surge una cuestión de si hay otras formas de re-etiquetar las caras de los dados con números enteros positivos que generan estas sumas con las mismas frecuencias. La sorprendente respuesta a esta pregunta es que no existe realmente tal manera. Estos son los dados Sicherman.
La siguiente tabla lista todos los posibles los totales de tiradas de dados con los dados estándar y dados Sicherman. Un dado Sicherman es de color para mayor claridad: 1-2 - 2 3 - 3 -4 , y el otro es todo negro, 1-3-4-5-6-8.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Dados estándar | 1 1 | 1 2 2 1 | 1 3 2 2 3 1 | 1 4 2 3 3 2 4 1 | 1 5 2 4 3 3 4 2 5 1 | 1 6 2 5 3 4 4 3 5 2 6 1 | 2 6 3 5 4 4 5 3 6 2 | 3 6 4 5 5 4 6 3 | 4 6 5 5 6 4 | 5 6 6 5 | 6 6 |
| Dados Sicherman | 11 | 2 1 21 | 3 1 3 1 13 | 1 4 2 3 2 3 41 | 1 5 2 4 2 4 3 33 3 | 1 6 2 5 2 5 3 4 3 44 3 | 2 6 2 6 3 5 3 54 4 | 1 8 3 6 3 6 45 | 2 8 2 8 46 | 3 8 38 | 48 |
Matemática Justificación
Deja que un canónica n unilateral morir sea un n -edro cuyos rostros están marcados con los números enteros [1, n] tales que la probabilidad de sacar cada número es 1 / n . Considere la cúbica canónica (seis lados) morir. La función de generación de la lanza de un dado tal es 
. El producto de este polinomio con sí mismo produce la función generatriz de la lanza de un par de dados: 
. Desde la teoría de polinomios ciclotómicos, sabemos que
. El producto de este polinomio con sí mismo produce la función generatriz de la lanza de un par de dados: . Desde la teoría de polinomios ciclotómicos, sabemos que
donde d se extiende sobre los divisores de n y 
es el d -th ciclotómico polinómica. Observamos también que
es el d -th ciclotómico polinómica. Observamos también que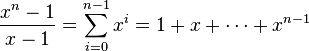
.
Por lo tanto, obtenemos la función de generación de un solo n die canónica unilateral como
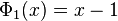y se cancela. Por lo tanto la factorización de la función de generación de una matriz canónica de seis caras es
La función de generación para los tiros de dos dados es el producto de dos copias de cada uno de estos factores. ¿Cómo podemos dividir para formar dos dados jurídicas cuyos puntos no están dispuestas tradicionalmente? Aquí legalessignifica que los coeficientes son no-negativo y suma a seis, de manera que cada dado tiene seis caras y cada cara tiene por lo menos un punto. (Es decir, la función de generación de cada matriz debe ser un polinomio p (x) con coeficientes positivos, y con p (0) = 0 y p (1) = 6.) Sólo existe una tal partición:
y
Esto nos muestra la distribución de las manchas en el rostro de un par de dados Sicherman como {1,2,2,3,3,4} y {1,3,4,5,6,8}, como antes.
Esta técnica puede ser extendido por los dados con un número arbitrario de lados.
No hay comentarios:
Publicar un comentario