En geometría, la espiral de Theodorus (también llamado espiral raíz cuadrada , espiral Einstein o espiral de Pitágoras ) es una espiral compuesta ofcontiguous triángulos rectángulos. Fue construido por primera vez por Theodorus de Cirene.
Construcción
La espiral se inicia con un triángulo rectángulo isósceles, con cada pata tiene unidad de longitud. Otro triángulo rectángulo está formado, de un triángulo automedian derecha con una pierna es la hipotenusa del triángulo antes (con longitud √ 2) y la otra pierna que tiene una longitud de 1, la longitud de la hipotenusa de este segundo triángulo es √ 3. El proceso se repite entonces, el i ª triángulo en la secuencia es un triángulo rectángulo con longitudes de los lados √ i y 1, y con √ hipotenusa ( i + 1).
Historia
Aunque toda la obra de Teodoro 'se ha perdido, Platón puso Theodorus en su diálogo Teeteto , que nos habla de su trabajo. Se supone que Theodorus había demostrado que todas las raíces cuadradas de números enteros no cuadrados entre 3 y 17 son irracionales por medio de la espiral de Theodorus.
Platón no atribuye la irracionalidad de la raíz cuadrada de 2 a Theodorus, porque era bien sabido que tenía delante.Theodorus y Teeteto dividen los números racionales y los números irracionales en diferentes categorías.
Hipotenusa
Cada uno de los triángulos 'hipotenusas h i da la raíz cuadrada del número natural correspondiente, con h 1 = √ 2.
Platón, bajo la tutela de Theodorus, se preguntó por qué se detuvo en Theodorus √ 17. La razón se cree ser que la hipotenusa √ 17 pertenece a la última triángulo que no se superpone la figura.
Superposición
En 1958, Erich Teuffel demostró que no hay dos hipotenusas alguna vez coinciden, sin importar qué tan lejos se continúa la espiral. Además, si los lados de longitud unitaria se extienden en una línea, ellos nunca pasar por cualquiera de los otros vértices de la figura total.
Extensión
Theodorus detuvo su espiral en el triángulo con una hipotenusa de √ 17. Si la espiral se continúa a un número infinito de triángulos, muchas de las características más interesantes se encuentran.
Índice de crecimiento
Ángulo
Si φ n es el ángulo de la N ª triángulo (o segmento de espiral), entonces:
Por lo tanto, el crecimiento de la φ ángulo N de la siguiente triángulo n es:
La suma de los ángulos de los primeros k triángulos se llama el ángulo total φ ( k ) para la k ª triángulo, y que es igual a:
con
Radio
El crecimiento del radio de la espiral en un cierto triángulo n es
Espiral de Arquímedes
La Espiral de Theodorus aproxima a la espiral de Arquímedes. Así como la distancia entre dos espiras de la espiral de Arquímedes es igual a constantpi matemática, como el número de giros de la espiral de Theodorus tiende a infinito, la distancia entre dos devanados consecutivos se acerca rápidamente π.
La siguiente es una tabla que muestra la distancia de dos arrollamientos del pi acercándose en espiral:
| Winding No.: | Media distancia sinuoso Calculado | Precisión de la media distancia de arrollamiento en comparación con π |
|---|---|---|
| 2 | 3.1592037 | 99,44255% |
| 3 | 3.1443455 | 99,91245% |
| 4 | 3.14428 | 99,91453% |
| 5 | 3.142395 | 99,97447% |
| → ∞ | → π | → 100% |
Como se muestra, después de sólo la quinta bobinado, la distancia es una aproximación exacta 99.97% a π.
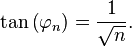




No hay comentarios:
Publicar un comentario