En teoría de números, la conjetura de Polignac fue hecha por Alphonse de Polignac en 1849 y afirma:
- Para cualquier número positivo incluso n , hay infinitamente muchas lagunas principales de tamaño n . En otras palabras: hay un número infinito de casos de dos números primos consecutivos con diferencia n .
La conjetura aún no ha sido probada ni refutada por un determinado valor de n . En el año 2013 un avance importante fue hecho por Zhang Yitang que probaron que hay infinitamente muchas lagunas principales de tamaño n para algún valor de n <70 millones.
Para n = 2, es la conjetura de primos gemelos. Para n = 4, se dice que hay infinitos números primos primos ( p , p + 4). Para n = 6, se dice que hay infinitos números primos sexy ( p , p + 6) sin privilegiada entre p y p + 6.
La conjetura de Dickson generaliza la conjetura de Polignac para cubrir todas las constelaciones principales, la conjetura Bateman-Horn da densidades asintóticas conjeturadas.
DENSIDAD CONJETURADO.
Que  incluso para n es el número de lagunas principales de tamaño n abajo x .
incluso para n es el número de lagunas principales de tamaño n abajo x .
 incluso para n es el número de lagunas principales de tamaño n abajo x .
incluso para n es el número de lagunas principales de tamaño n abajo x .
La primera conjetura de Hardy-Littlewood dice la densidad asintótica es de forma
donde C n es una función de n , y 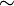 significa que el cociente de dos expresiones tiende a 1 como x tiende a infinito. [ cita requerida ]
significa que el cociente de dos expresiones tiende a 1 como x tiende a infinito. [ cita requerida ]
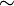 significa que el cociente de dos expresiones tiende a 1 como x tiende a infinito. [ cita requerida ]
significa que el cociente de dos expresiones tiende a 1 como x tiende a infinito. [ cita requerida ]
C 2 es la constante de primos gemelos
donde el producto se extiende sobre todos los números primos p ≥ 3.
C N es C 2 multiplicado por un número que depende de los factores primos impares Q de n :
Por ejemplo, C 4 = C 2 y C 6 = 2 C 2 . Primos gemelos tienen la misma densidad conjeturada como primos primos, y la mitad del de los números primos sexy.
Tenga en cuenta que cada factor primo impar q de N aumenta la densidad conjeturado en comparación con primos gemelos por un factor de  . Un argumento heurístico sigue.
. Un argumento heurístico sigue.
 . Un argumento heurístico sigue.
. Un argumento heurístico sigue.
Se basa en algunos supuestos no probados por lo que la conclusión sigue siendo una conjetura. La probabilidad de que un primo impar aleatoria q dividir ya sea un o una + 2 en un "potencial" par gemelo prima al azar es  , ya q divide a 1 de los q números de una a una + q - 1.
, ya q divide a 1 de los q números de una a una + q - 1.
 , ya q divide a 1 de los q números de una a una + q - 1.
, ya q divide a 1 de los q números de una a una + q - 1.
Ahora supongamos q divide n y considerar un par primer potencial ( un , una + N ). q divide un + n si y sólo si q divide una , y la probabilidad de que es  . La probabilidad de que ( una , un + n ) estar libre de el factor q , dividido por la probabilidad de que ( una , un + 2 ) está libre de Q , a continuación, se convierte
. La probabilidad de que ( una , un + n ) estar libre de el factor q , dividido por la probabilidad de que ( una , un + 2 ) está libre de Q , a continuación, se convierte  dividido por
dividido por  .
.
 . La probabilidad de que ( una , un + n ) estar libre de el factor q , dividido por la probabilidad de que ( una , un + 2 ) está libre de Q , a continuación, se convierte
. La probabilidad de que ( una , un + n ) estar libre de el factor q , dividido por la probabilidad de que ( una , un + 2 ) está libre de Q , a continuación, se convierte  dividido por
dividido por  .
.
Esto es igual  que transfiere a la densidad primer conjeturado. En el caso de n = 6, el argumento se simplifica a: Si una es un número aleatorio a continuación 3 tiene la oportunidad de 2/3 de dividir una o un 2 +, pero única oportunidad tercio de dividir una y un + 6, por lo que el Este último par se conjetura doble de probabilidades de ser ambos primos.
que transfiere a la densidad primer conjeturado. En el caso de n = 6, el argumento se simplifica a: Si una es un número aleatorio a continuación 3 tiene la oportunidad de 2/3 de dividir una o un 2 +, pero única oportunidad tercio de dividir una y un + 6, por lo que el Este último par se conjetura doble de probabilidades de ser ambos primos.
 que transfiere a la densidad primer conjeturado. En el caso de n = 6, el argumento se simplifica a: Si una es un número aleatorio a continuación 3 tiene la oportunidad de 2/3 de dividir una o un 2 +, pero única oportunidad tercio de dividir una y un + 6, por lo que el Este último par se conjetura doble de probabilidades de ser ambos primos.
que transfiere a la densidad primer conjeturado. En el caso de n = 6, el argumento se simplifica a: Si una es un número aleatorio a continuación 3 tiene la oportunidad de 2/3 de dividir una o un 2 +, pero única oportunidad tercio de dividir una y un + 6, por lo que el Este último par se conjetura doble de probabilidades de ser ambos primos.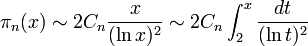

No hay comentarios:
Publicar un comentario