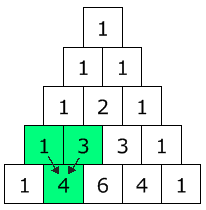
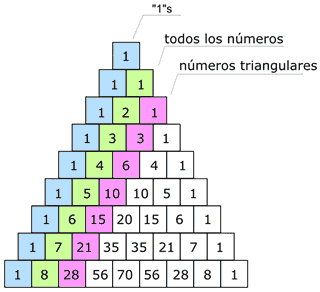
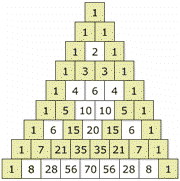
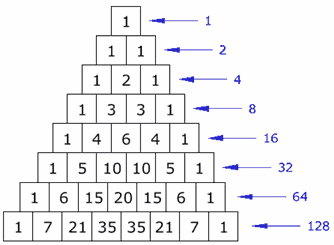
Encontré este
artículo donde nos brindan 10 tips para enseñar efectivamente matemáticas en
secundaria. Lo traduzco y resumo para ustedes:
1. Haz que el contenido sea
irresistible
La principal pregunta que surge en un
estudiante cansado y desmotivado es: ¿Para qué estudio algo que no voy a
utilizar nunca? Tu deber como docente es demostrar para qué les va a servir lo
que están aprendiendo y cómo pueden ponerlo en práctica. Con un poco de
investigación y planeamiento podemos descubrir cuáles son los temas de
actualidad que pueden interesar a los alumnos. Por poner un ejemplo,
aprovechando el tema de las olimpiadas se puede introducir el estudio de los
ángulos, investigando en qué ángulo debe viajar la jabalina para llegar más
lejos. O sea, sacar las matemáticas del libro y aplicarlas a un tema de
interés.
2. No premies a tus estudiantes
con dulces
(O stickers, o demás tipos de premios) No hay
por qué dar la idea de que las matemáticas son tan aburridas que debes
motivarlos con un premio. Si sigues el tip número 1 no necesitarás motivarlos
con dulces.
3. Crea y promueve el trabajo en
equipo
Los alumnos que gustan más de la materia pueden
ser de mucha ayuda para explicar y ayudar personalmente a sus compañeros.
4. Calidad antes que cantidad
Es preferible dejar menos trabajos y tareas
que tengan mayor importancia en cuanto al aprendizaje y práctica del contenido.
Mucho trabajo sin sentido solo logrará cansar al alumno.
5. Enseña y modela el proceso de
pensamiento y resolución
Algunas veces podemos caer en el tentación de
dar las respuestas, o valorar más al alumno que llega a ellas sin explicar cómo
lo hizo. Es más importante que todos sean capaces de lograr un entendimiento
del proceso, aunque la respuesta no sea exacta.
6. Menos calificación y más
crítica constructiva
Al alumno le sirve más una explicación de en
qué se equivocó y cómo puede enmendar el error, que una simple calificación.
7. Invierte la forma de pensar
Un excelente ejemplo de este tip se da con los
problemas, en vez de darle 100 problemas para que aprendan a resolverlos,
pídeles que creen 10 problemas sacados de situaciones cotidianas personales. Al
tener que crear el problema a partir de la solución les será mucho más sencillo
entender el proceso.
8. Cuenta cuentos
Los cuentos son una excelente forma de atraer
la atención de los alumnos, además sirven de background para cualquier
operación matemática, dándole sentido.
9. Programa tutorías semanales a
los alumnos menos aventajados antes de las evaluaciones. (ver tip 3)
10. Trabaja con las emociones
Pregunta cómo se sienten sobre la clase de
matemáticas, es normal que a algunos les aburra y a otros les guste. Lo
importante es escuchar dónde está la mayoría, algunos días puede que estén más
cansados y otros días más animados. Tu plan de clase puede adaptarse a sus
emociones, si están aburridos, intentar una actividad que les pueda divertir
más; si están cansados, poner menos trabajo o aprovechar para poner en práctica
el tip 8, etc.
Espero que les sirva para sus hacer sus clases
de Matemáticas más divertidas.