LA REGLA DE CRAMER

En álgebra lineal, la regla de Cramer es una fórmula explícita para la solución de un sistema de ecuaciones lineales con tantas ecuaciones como incógnitas, válidas siempre que el sistema tiene una solución única. Expresa la solución en términos de los factores determinantes de la (plaza) y la matriz de coeficientes de las matrices obtenidas de la misma mediante la sustitución de una columna por el vector de lados derechos de las ecuaciones. Lleva el nombre de Gabriel Cramer (1704-1752), que publicó la norma para un número arbitrario de incógnitas en 1750, aunque Colin Maclaurin también publicó los casos especiales de la norma en 1748 (y posiblemente sabía de él tan pronto como 1729).

CASO GENERAL.

Considere la posibilidad de un sistema de  n  ecuaciones lineales para n  incógnitas, representado en forma de multiplicación de matrices de la siguiente manera:

donde el  N  por  N  de la matriz   tiene un determinante distinto de cero, y el vector   es el vector columna de las variables.

Entonces el teorema afirma que en este caso el sistema tiene una solución única, cuyos valores individuales para las incógnitas están dados por:

donde   es la matriz formada por la sustitución de la  i -ésima columna de   la columna por el vector  .

La regla es válida para sistemas de ecuaciones con coeficientes y las incógnitas en cualquier campo, no sólo en los números reales. Se ha demostrado recientemente que la regla de Cramer se puede implementar en O ( n 3 ) el tiempo, que es comparable a los métodos más comunes de sistemas de ecuaciones lineales, tales eliminación asGaussian resolver.

PRUEBA.

La prueba para la regla de Cramer utiliza sólo dos propiedades de determinantes: linealidad con respecto a cualquier columna dada (teniendo para esa columna una combinación lineal de vectores de columna produce como determinante la correspondiente combinación lineal de sus determinantes), y el hecho de que el determinante es cero Siempre que las dos columnas son iguales (que está implícito en la propiedad básica que el determinante es alterna en las columnas).

Fijar el índice  j  de una columna. La linealidad significa que si tenemos en cuenta sólo la columna  j  como variables (que se fijan los demás arbitrariamente), la función resultante  R n  →  R  (suponiendo entradas de la matriz están en  R ) puede ser dada por una matriz, con una fila y  n  columnas, que actúa en la columna  j . De hecho, esta es precisamente la expansión whatLaplace hace, escribiendo det ( A ) = C 1 a 1, j  + ... +  C n un n , j  para determinados coeficientes  C 1 , ..., Cn  que dependen de las columnas de  A  que no sea la columna  j  (la expresión exacta de estos cofactores no es importante en este caso).El DET valor ( A ) es entonces el resultado de la aplicación de la matriz de una línea L ( j )  = ( C 1  C 2  ...  C n ) a la columna  j  de  A . Si  L ( j ) se aplica a cualquier  otra  columna  k  de  A , entonces el resultado es el determinante de la matriz obtenida a partir  Un  mediante la sustitución de la columna  j  de una copia de la columna  K , por lo que el factor determinante resultante es 0 (el caso de dos igual columnas).

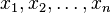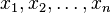Consideremos ahora un sistema de  n  ecuaciones lineales con  n incógnitas  , cuya matriz de coeficientes es  A , con det ( A ) se supone que es distinto de cero:

Si uno combina estas ecuaciones tomando  C 1  veces la primera ecuación, además de  C 2  veces el segundo, y así sucesivamente hasta  C n  veces el pasado, entonces el coeficiente de  x j  se convertirá en  C 1 a 1, j  + ... +  C n un N , j  = det ( A ), mientras que los coeficientes de todos los demás incógnitas se convierten en 0, el lado izquierdo se convierte simplemente en det ( A ) x j . El lado derecho es C 1 b 1  + ... +  C n b n , que es  L ( j )  aplicada al vector columna  b de los lados derecho e  b i . De hecho lo que se ha hecho aquí es multiplicar la ecuación matricial  A  ⋅  x  =  b  en la dada por  L ( j ) . Al dividir por el número distinto de cero det ( A ) se encuentra la siguiente ecuación, necesaria para satisfacer el sistema:

Pero por la construcción del numerador es el determinante de la matriz obtenida de  A  mediante la sustitución de la columna  j  por  b , por lo que tenemos la expresión de la regla de Cramer, como condición necesaria para una solución. El mismo procedimiento se puede repetir para otros valores de  J  para encontrar valores para las otras incógnitas.

El único punto que queda por demostrar es que estos valores de las incógnitas, las únicas posibles, en efecto, forman juntos una solución.Pero si la matriz  A  es invertible con inversa  Un -1 , entonces  x  =  A-1  ⋅  B  será una solución, mostrando así su existencia. Para ver que A  es invertible cuando det ( A ) es distinto de cero, considere la  N por  N  de la matriz  M  obtenido por el apilamiento de la de una línea matrices  L ( j )  en la parte superior de uno al otro para  j  = 1, 2, ...,  n (este da la matriz adjugate para  A ). Se demostró que la  L ( j )  ⋅  A  = (0 ... 0 det ( A ) 0 0 ...) donde det ( A ) aparece en la posición  j , de donde se sigue que M  ⋅  A  = det ( A ) I n . Por lo tanto