Pitágoras, filosofía y matemáticas.

 

Pitágoras nació en la isla de Samos (Grecia), en el 570 a. C. y murió en Metaponto en el 469 a. C., hijo de Mnesarco. Fue discípulo de Tales  y de Fenecidas de Siria, estudió en la escuela de Mileto. Viajó por Oriente Medio (Egipto y Babilonia). Sufrió el exilio para escapar de la tiranía del dictador Samio Polícrates, por lo que vagabundeó hasta establecerse  en el 531 a. C. en las colonias italianas de Grecia donde fundó su famosa escuela pitagórica en Crotona al sur de Italia. Se cree que inventó (si no él sus discípulos), las tablas de multiplicar y que fue el primero en demostrar el conocido Teorema de Pitágoras sobre la relación entre los lados de un triángulo rectángulo, aunque ya los egipcios y los babilonios lo usaban en sus cálculos, construcciones,  entre otros sin haberlo demostrado. Pitagoras hizo diferentes aportes en las matematicas fue uno de los filosofos y matemáticos que le dio importancia amplia a los nuúmeros e hizo aporte tanto en las matemáticas como en algunas otras áreas no tan estrictas dentro de las ciencias como es la numerología.

Desde tiempos remotos, los números acompañan a la humanidad que, con grafismos atractivos o despreciables, han ido moldeando el significado de los mismos. Por supuesto, estas preferencias antiguas sobre los números refiere a cuestiones históricas, cabalísticas, científicas o supersticiosas que rigieron en cada tiempo y que, a lo largo de los siglos, se mantuvieron más o menos firmes acercándonos esa información y uso sobre los números.

“Todas las cosas son números”.
Pitágoras

Pero como los números son tan importantes para la humanidad, más de una ciencia o estudio se basaron en ellos; por supuesto, no hablaremos de las Matemáticas o la Física sino del estudio de esos números y su incidencia en el mundo y las personas.

Ciertamente, puede decirse a esta altura que el sustento científico no acompaña a estos análisis y que, por tanto, la información surgida del análisis de la “vibración de los números” carece de este rigor. Sin embargo esta disciplina, este arte adivinatorio, que se remonta hasta el mismo Pitágoras -y los Pitagóricos- habla del poder de los números y fundamenta en un conjunto de creencias y tradiciones que se han defendido desde antes del Cristianismo y que luego la Biblia recogió y que podemos ver, incluso, en la kabbalah.

Se trata de mística, de fuerzas espirituales entre símbolos, personas y hechos y, por tanto de un sistema de creencias (fe) necesario para sostener su validez.

“El conocimiento matemático ha sido considerado por mucho tiempo como un paradigma del conocimiento humano con verdades que son a la vez necesarias y ciertas, por lo que dar una explicación del conocimiento matemático es una parte importante de la epistemología. Los objetos matemáticos, tales como los números y los conjuntos, son ejemplos arquetípicos de abstracciones, dado que el tratamiento de tales objetos en nuestro discurso es como si fueran independientes del tiempo y el espacio, encontrar un lugar para los objetos de este tipo en un marco más amplio del pensamiento es una tarea central de la ontología, o metafísica. El rigor y la precisión del lenguaje matemático depende del hecho de que está basado en un vocabulario limitado y gramática muy estructurado, y las explicaciones semánticas del discurso matemático a menudo sirven como punto de partida de la filosofía del lenguaje. Aunque el pensamiento matemático ha demostrado un alto grado de estabilidad a través de la historia, su práctica también ha evolucionado con el tiempo, y algunos desarrollos han provocado controversia y debate; clarificar los objetivos básicos de esta práctica y los métodos apropiados es, por lo tanto, una la tarea metodológica y  fundacional importante, situando la filosofía de las matemáticas dentro de la filosofía general de la ciencia¨.

Entre los aportes a la ciencia encontramos el teorema de pitagoras. Que se explica brevemente en el siguiente video.

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

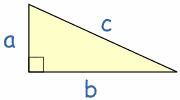Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2

Tarea
Poblemas a resolver