MATEMÁTICAS DIVERTIDAS
Primero que nada les doy las
gracias por darse la oportunidad de checa este blog, que desde mi punto de
vista te agradara y servirá para aprender de forma divertida las operaciones básicas en ARITMÉTICA, que sin duda alguna para poder entender temas mas avanzados necesitas lo básico y yo te lo presentare en forma dinámica y no tan aburrida, dejar a un lado ese temor y vamos a echarle un vistazo.
Tu opinión o comentarios
respecto a este material son importantes
para mejorarlo.
PARA COMENZAR REALIZARAS EL SIGUIENTE EJERCICIO DE GIMNASIA CEREBRAL, TE DARÁS CUENTA LO FÁCIL QUE ES Y LO DIVERTIDO DE APRENDER MATEMÁTICAS.
Los investigadores afirman que el ejercicio, además de mantener en forma huesos, músculos, corazón y pulmones, también fortalece el ganglio basal, el cerebelo y el cuerpo calloso del cerebro. Además, cuando re realiza en forma coordinada, provoca el incremento de neuroendocrina y un gran número de conexiones entre las
neuronas. Esta Gimnasia Cerebral® mantendrá tu cuerpo/mente balanceado para aprender. En este ejercicio te explicaré su rutina, para qué sirve.
PASOS
1. Utiliza una hoja grande de papel y un lápiz; pega la hoja en la pared al nivel de tus ojos.
2. Dibuja un ocho acostado (∞) empezando por el centro (donde se cruzan las líneas) y de ahí hacia arriba a la derecha.
3. Cada vez que muevas tu mano el ojo debe seguir ese movimiento; si tu ojo tiende a ir más rápido que tu mano, aumenta la velocidad de está; lo importante es que tu ojo siga a tu mano y no la pierda de vista.
4. Repite tres veces esta movimiento sobre el mismo ocho que dibujase inicialmente.
5. Usando tu ocho inicial cambia a la dirección contraria (abajo a la izquierda).
6. Repite tres veces este movimiento.
7. Usa: “Música para Aprender Mejor” (Selección: Música para Revitalizar el Cerebro)
BENEFICIOS
VER FIGURA
Listo espero te sirva para despejar tu mente, comencemos¡¡¡¡¡
PARA COMENZAR REALIZARAS EL SIGUIENTE EJERCICIO DE GIMNASIA CEREBRAL, TE DARÁS CUENTA LO FÁCIL QUE ES Y LO DIVERTIDO DE APRENDER MATEMÁTICAS.
Los investigadores afirman que el ejercicio, además de mantener en forma huesos, músculos, corazón y pulmones, también fortalece el ganglio basal, el cerebelo y el cuerpo calloso del cerebro. Además, cuando re realiza en forma coordinada, provoca el incremento de neuroendocrina y un gran número de conexiones entre las
neuronas. Esta Gimnasia Cerebral® mantendrá tu cuerpo/mente balanceado para aprender. En este ejercicio te explicaré su rutina, para qué sirve.
PASOS
1. Utiliza una hoja grande de papel y un lápiz; pega la hoja en la pared al nivel de tus ojos.
2. Dibuja un ocho acostado (∞) empezando por el centro (donde se cruzan las líneas) y de ahí hacia arriba a la derecha.
3. Cada vez que muevas tu mano el ojo debe seguir ese movimiento; si tu ojo tiende a ir más rápido que tu mano, aumenta la velocidad de está; lo importante es que tu ojo siga a tu mano y no la pierda de vista.
4. Repite tres veces esta movimiento sobre el mismo ocho que dibujase inicialmente.
5. Usando tu ocho inicial cambia a la dirección contraria (abajo a la izquierda).
6. Repite tres veces este movimiento.
7. Usa: “Música para Aprender Mejor” (Selección: Música para Revitalizar el Cerebro)
BENEFICIOS
- Mejora la comunicación escrita.
- Establece el ritmo y fluidez necesarios para una buena coordinación mano/ojo.
- Estimula los músculos más largos de los ojos y la alerta táctil.
- Relaja los músculos de manos, brazos y hombros, y facilita el proceso de visión.
- Ayuda a la integración colateral del pensamiento(conexión de ambos hemisferios cerebrales).
- Favorece el que las ideas fluyan fácilmente.
VER FIGURA
Listo espero te sirva para despejar tu mente, comencemos¡¡¡¡¡
¿QUE SON LAS MATEMÁTICAS?
Es una ciencia formal que, partiendo de axiomas y siguiendo el
razonamiento lógico, estudia las propiedades y relaciones entre entidades
abstractas (números, figuras geométricas). Las matemáticas se emplean para estudiar relaciones cuantitativas,
estructuras, relaciones geométricas y las magnitudes.
¿DONDE USAMOS LAS MATEMÁTICAS?
Hoy en día, las matemáticas se usan en todo el mundo como una
herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales la ingeniería la medicina y las ciencias sociales e incluso disciplinas que, aparentemente, no están vinculadas con
ella, como la música.
¿PARA QUE SIRVEN LOS NÚMEROS?
Piensa en todas las cosas donde existen los números,
¿son muchas verdad? Observa y contesta el siguiente ejemplo.
¿Para qué no sirven los números en un calendario?
¿Para qué nos sirven los números en el celular?
¿Para qué nos sirven los números en el reloj?
OPERACIONES BÁSICAS DE LA ARITMÉTICA.
TE SUGIERO ESTE VÍDEO PARA QUE RECUERDES LAS OPERACIONES BÁSICAS.
TE PRESENTO ESTE MATERIAL PARA SUMAR, RESTAR, MULTIPLICAR Y DIVIDIR MAS RÁPIDO DE LO QUE PUEDES IMAGINAR Y ES MUY SENCILLO.
EL SIGUIENTE VÍDEO ES UN MATERIAL DIDÁCTICO PARA APRENDER LAS TABLAS DE MULTIPLICAR MAS RÁPIDO Y DE FORMA DIVERTIDA.
Existen muchas formas de aprendernos las tablas de multiplicar, pero la forma mas rápida de aprenderlas es con canciones, juegos, dinámicas es por ello que te dejo este material esperando que lo realices con tus compañeros de clases.
FRACCIONES DIVERTIDAS
Aprende Las Fracciones
Una fracción, en general, es la expresión de una cantidad dividida por otra, y una fracción propia representa las partes que tomamos de un todo.
El ejemplo clásico es el de un queso que partimos en porciones. En el dibujo, hemos hecho 8 porciones, 3 rosas y 5 verdes.
| Si tomamos las 3 rosas, representan 3 porciones de las ocho en las que hemos dividido el queso, es decir 3 / 8 del queso, y si tomamos las 5 verdes, representan 5 porciones de las ocho en las que hemos dividido el queso, es decir 5 / 8 del queso. |  |
Las partes que tomamos ( 3 ó 5 ) se llaman numerador y las partes en que dividimos el queso 8 denominador.
Clasificación De Las Fracciones
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.
| Tipo | Características | Ejemplos |
| Propia | El numerador es menor que el denominador | 1 / 2, 7 / 9 |
| Impropia | El numerador es mayor que el denominador | 4 / 3, 5 / 2 |
| Homogéneas | Tienen el mismo denominador | 2 / 5, 4 / 5 |
| Heterogéneas | Tienen distinto denominador | 3 / 7, 2 / 8 |
| Entera | El numerador es igual al denominador; representan un entero | 6 / 6 = 1 |
| Equivalentes | Cuando tienen el mismo valor. Dos fracciones son equivalentes si son iguales sus productos cruzados | 2 / 3 y 4 / 6 2 x 6 = 3 x 4 |
TOMANDO EN CUENTA LO ANTERIOR TE RECOMIENDO VEAS EL SIGUIENTE VÍDEO QUE AYUDARA A ENTENDERLAS AUN MAS.
Si en una fracción multiplicamos o dividimos el numerador y el denominador por un mismo numero, obtenemos una fracción equivalente a la primera, pues ambas tienen el mismo valor. Por ejemplo:
| 1 | (1 x 4) | 4 | 3 | (3 : 3) | 1 | |||||||||
| — | = | ——— | = | — | = | 0,5 ; | — | = | ——— | = | — | = | 0,2 | |
| 2 | (2 x 4) | 8 | 15 | (15 : 3) | 5 |
Simplificar o Reducir una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, lo primero que hacemos es buscar el mayor número que divide exactamente (resto = 0) al numerador y al denominador (mayor divisor común) y después dividimos el numerador y el denominador por este mayor divisor común, ya que como hemos visto antes, dividiendo el numerador y el denominador de una fracción por un mismo número obtenemos una fracción equivalente (de igual valor).
Por ejemplo: Simplificar 30/42
Los números que dividen exactamente a 30 (divisores) son: 2, 3, 5, 6, 10 y 15.
Los números que dividen exactamente a 42 (divisores) son: 2, 3, 6, 7, 14 y 21.
Los divisores comunes a ambos son 2, 3 y 6. El mayor divisor común es 6, por tanto, dividimos numerador y denominador por 6.
| 30 | 30/6 | 5 | ||
| —— | = | ——— | = | — |
| 42 | 42/6 | 7 |
Cuando en una fracción, el numerador y el denominador no tienen ningún divisor común, se dice que es una fracción irreducible.
A CONTINUACIÓN TE PRESENTO TRES VÍDEO DE LAS OPERACIONES BÁSICAS CON FRACCIONES. ESPERO LOS ENTIENDAS.
NÚMEROS DECIMALES
¿Qué son los números decimales? Los números decimales se utilizan para representar números más pequeños que la unidad.
Los números decimales se escriben a la derecha de las Unidades separados por una coma. Es decir:
Centenas Decenas Unidades , Décimas Centésimas Milésimas
En la imagen que aparece a continuación, el primer cuadrado representa la Unidad. Si esta unidad la dividimos en 10 partes iguales (segundo cuadrado), representaremos las Décimas. Si las décimas las dividimos en 10 partes iguales o la unidad en 100 partes iguales (tercer cuadrado), representaremos las Centésimas.

Veamos algunos ejemplos:
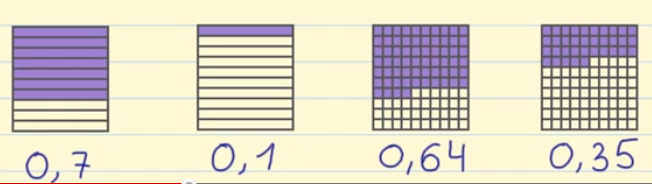
Primer ejemplo: Si la unidad la dividimos en 10 partes iguales, tendremos décimas. Y hemos coloreado 7 de estas partes. La forma de escribirlo es 0 unidades,7 décimas = 0,7
Segundo ejemplo: En el segundo ejemplo también tenemos décimas y tenemos coloreadas 1. Se escribirá de la siguiente forma: 0 unidades,1 décima = 0,1
Tercer ejemplo: En el tercer ejemplo tenemos representadas centésimas, de las cuales tenemos coloreadas 6 décimas y 4 centésimas. Por lo tanto se escribirá: 0 unidades,6 décimas 4 centésimas = 0,64
Cuarto ejemplo: Tenemos centésimas (la unidad entre 100), de las cuales tenemos coloreadas 3 décimas y 5 centésimas. Lo escribiremos: 0 unidades,3 décimas 5 centésimas = 0,35
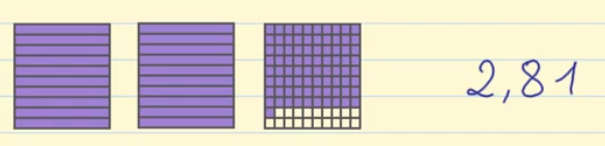
Quinto ejemplo: Tenemos dos unidades enteras coloreadas y de la tercera unidad, que está dividida en centésimas, tenemos 8 décimas coloreadas y una centésima coloreada. Por lo tanto, se escribirá: 2 unidades,8 décimas 1 centésimas = 2,81
¿Cual es la relación de los decimales con las fracciones?
La Unidad se representa por 1.
La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001
Ejemplo para pasar de decimal a fracción:
7,508:
Nos fijamos en el último número, en el 8, que ocupa el lugar de las milésimas, por lo tanto el denominador tendrá que ser 1000. Y en el numerador escribiremos el número completo sin la coma. 7,508 = 7508/1000
Ejemplo para pasar de fracción a decimal:
402/100:
Como el denominador es 100, el último número del numerador (el 2) , tiene que ser las centésimas, el anterior (el 0) tienen que ser las décimas y el anterior a éste (el 4) tiene que ser las unidades, poniendo la coma detrás de las unidades. Por lo tanto, 402/100 = 4,02
RAZÓN Y PROPORCIÓN.
Para saber que es una razón, una proporción y donde aplicar las proporciones de manera divertida ponle música a tus oídos y dale click al siguiente URL.
POTENCIACIÓN
La potenciación es una multiplicación de varios factores iguales, al igual que la multiplicación es una suma de varios su mandos iguales, (la potenciación se considera una multiplicación abreviada).
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente, que se escribe en forma de superíndice. El exponente determina la cantidad de veces que la base se multiplica por sí misma.
Por ejemplo:
En general:
Normalmente, las potencias con base 10, por la cantidad que represente el exponente, esa será la cantidad de ceros en el resultado. El resto de la bases, para sacar el resultado el número se multiplica por sí mismo cuantas veces indique el exponente.
Checa el siguiente vídeo donde te mostrare algo de potenciación.
Bueno con estó termina mi blog espero te haya servido de mucho, espero tus comentarios.









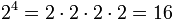
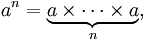
BUENA INFORMACION ;)
ResponderEliminarMuchas gracias Maribel¡¡¡
Eliminarexcelente aportacion sobre las matematicas, muy interesante!!
ResponderEliminarGracias Lucy saludos¡¡¡
Eliminar